数学高考模拟试卷（新课程卷）

数学高考模拟试卷（新课程卷）

一选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合M={直线}，N={圆}，则M∩N的元素个数为（　　  ）

A．0　　　 B．1　　　　C．2　　　　D．以上都有可能

2．已知集合M={a，b，c}，N={—1，0，1}，若f是M→N的映射，且f（a）=0，则这样的映射f共有（　　　）A．4个　　　 B．6个　　  C．9个　　　 D．27个

3．下列四个函数中，同时具有性质：（1）最小正周期是π；（2）图象关于直线对称，则这个函数是（　　  ）

A．　B．　C．　　D．

4．若x、yR，则x<1,y<1是 x+y+x-y<2成立的（　　　）

A．充分不必要条件　 B．必要不充分条件　C．充要条件　　D.不充分不必要条件

5 若　 ，则下列不等式　　　　　　　　　　　

（1）． （2）． （3）． （4）．

其中成立的个数为（　 ）A．0　　 B。1　C.2　　D.3

6．设两个独立事件A和B都不发生的概率为，A发生B不发生的概率与B发生但A不发生的概率相同，则事件A发生的概率P（A）是（　　  ）

A．　　　 B．　　　 C．　　　　D．

7．已知线段AD∥平面α，且在平面α的距离等于4，点B是平面α内动点，且满足AB=5，若AD=10，则点D与点B的距离d满足（　　）

A、d的最大值为，无最小值　　　　B、d的最小值为，无最大值

C、d的最大值为，最小值　　  D、d的最大值为，最小值为

8．等差数列{a_n}前n项和为S_n，满足S₂₀=S₄₀则下列结论中正确的是（　　　）

A．S₃₀是S_n中最大值　　B．S₃₀是S_n中最小值　　 C．S₃₀ =0　　D．S₆₀=0

9．若f（x）是R上的减函数，且f（x）的图象经过点A（0，4）和点B（3，2），则

不等式的解集为（—1，2）时，a的值为（　　  ）

A．0　　　 B．—1　　　　C．1　　　　D．—2

10．图中多面体是过正四棱柱的底面正方形ABCD的点A作截面AB₁C₁D₁而截得的，且BB₁+DD₁=CC₁，已知线段AC₁与底面成30⁰，AB=1，则这个多面体的体积为（　　 ）

A．　　B．　　C．　　D．

11．若圆锥曲线C的过焦点的弦为直径的圆与它的相应准线有两个不同的交点,则曲线C一定是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　　 ） A.椭圆　 B.双曲线　 C.抛物线　 D.无法确定

12．某书店发行一套教学辅导书，定价每套20元，为促销，该书店规定：购买不超过50套，按定价出售；购买51至100套，按定价9折付款，购买超过100套，按定价8折付款。用n表示购书套数，有多少个n，会出现买多于n本书比恰好买n本书所付的钱还少？（　　 ）

A、5　　　　  B、10　　　　C、15　　　 D、16

二．填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

13．甲．乙．丙．丁四人参加奥运会射击项目选拔赛，四人的平均成绩和方差如下列所示

	甲	乙	丙	丁
平均环数	8.5	8.8	8.8	8
方差S2	3.5	3.5	2.1	8.7

则参加奥运会最佳人选应为________________

14．已知向量=（1，），=（），若正数k和t使得 =+（t²+1）  与垂直，则k最小值是__________

15．若曲线y=与y=x+2有且只有一个公共点P,O为坐标原点,则OP²的取值范围是____________

16．给出下列四个函数

（1） （2）　（3）　（4）

其中在[2，+∞]上是增函数的函数序号为__________

三．解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。

17．（本小题满分12分）

有一个表面都涂有红颜色的正方体，被均匀地锯成了1000个小正方体，将这些小正方体混合后，放入一个口袋。

（1）从口袋中任取一个正方体，恰有两个面涂有红色有概率是多少？

（2）从口袋中任取两个正方体，其中至少有一个是表面上有红色的概率是多少？

18．（本小题满分12分）

已知A是△ABC的内角,试比较2sin2A与tan的大小.

19．（本小题满分12分）

已知三棱锥S—ABC的底面是正三角形，A点在侧面SBC上的射影H是△SBC的垂心，二面角H—AC—C的平面角等于30⁰，SA=

（1）设O为S在平面ABC上的射影

（2）求三棱锥S—ABC的体积

20．（本小题满分12分）

已知双曲线C的两条渐近线经过坐标原点，且与以A（）为圆心，1为半径的圆相切，双曲线C的一个顶点A’与点A关于直线y=x对称。

（1）求双曲线C的标准方程；

（2）是否存在过A点的一条直线交双曲线C于两点M．N，且线段MN被直线x=-2平分？若存在，求出此直线；若不存在，说明理由。

21．（本小题满分12分）

设函数

（1）求

（2）若当时，值域为，求实数a的取值范围。

22（本小题满分14分）

比数列{a_n}的首项为,公比是展开式中的第2项

(1)　  用n和x表示数列{a_n}通项a_n

(2)　  若{a_n}前n项和为S_n, 求(A_n用n和x表示)

(3)　  当x>1时，若，求x

高考模拟试卷答案

一．选择题：

A　C  D　C　B　　　 D　D  D　C　D  B　D

二．填空题：

13．丙　　　14．2　　　15． 16．（1）．（3）

简解或提示：

1、 存在既是直线又是圆的圆锥曲线，故M∩N中没有元素

2、　　各有3种选择，故共9种映射

3、由将代入C，不是最值，故选D；

4、1⁰若成立，

若　 ∴

若　

∴

2⁰若，则

∴， 　 ∴

故选C

5、取，可排除（1）（3）（4），故选B

6、由题意，

　 　 ∴　

∴　　　　∴

7、如图，A’、D’分别是A、D的射影，

B的轨迹是以A’为圆心，3为半径的圆，连

A’D’，交圆于M、N，则DM为最大值，DM

=

DN为最小值，DN=　　故选D

8、由S₂₀=S₄₀，　 ∴　　∴

∴S₆₀=0　　　选D

9、　　 ∴　

∴　 又在R上为减函数

∴　　　　 ∴

而　　 ∴　　　 选C

10、将两个这样的多面体反扣在一起组成一个正四棱柱，易求得高为

∴　　 选D

11、如图，设圆锥曲线离心率为e，弦AB中点H，

分别向准线L作垂线，垂足为A’、B’、H’

∵图与直线相交，则HH’<r，　　　∴　　　　  ∴即为双曲线，选B

12、购买n本书所付总款额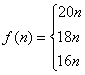　

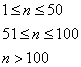
设买多于n本书时所付钱比恰好买n本书还少，则必有

　　　　　　或　

　　　　 　　　或　　

∴这样的n共有5 + 11= 16个

14、由，

则

　

由得

　 ,　 ∴　　∴k最小值为2。

15、如图，是圆心（a，0），半径为1 的上半圆，为直线；

当半圆与直线相切时，此时

当半圆与直线相交时，时只有一个交点，

∴

16、逐个讨论函数，对（1）：

则上为增函数；

对（2）：时，，函数无意义；

对（3）：在[2，+∞]上是增函数；

对（4）：时无意义

三．解答题：

17．解：（1）从口袋中任取一个正方体，恰有两个面涂有红色的概率是

　　　　　 

（2）从口袋中任取两个正方体，两个正方体表面上都没有颜色的概率为

　　　　　

其中至少有一个表面上有红色的概率为

18.解:∵A是△ABC的内角　 ∴A∈(0 , π)

　　 2sin2A－ tan

　 =4sinAcosA－

　 = (4sin²AcosA－1－cosA)

　 = [4(1－cos²A)cosA－(1+cosA)]

　 = (4cosA－4cos²A－1)

　 =

　 ∵A∈(0 , π) ∴sinA>0 , 1+cosA>0

 ∴2 sin2A－ tan≤0

当且仅当A=60°时2sin2A=tan

19．（1）由题设，AH⊥面SBC，作BH⊥SC于E，由三垂线定理可知SC⊥AE，SC⊥AB，故SC⊥面ABE，设S在面ABC内射影为O，则SO⊥平面ABC，由三垂线定理之逆定理，可知CO⊥AB于F，同理BO⊥AC，故O为△ABC的重心。

（2）又∵△ABC是等边三角形，故O为△ABC的中心，从而SA=CB=SC=

∵CF⊥AB，CF是EF在面ABC上的射影，由三垂线定理，EF⊥AB

∴∠EFC是二面角H—AB—C的平面角

故∠EFC=30⁰　 OC=SC·COS60⁰=

SO=

又OC= 故AB=

∴

20．解（1）如图设切点为B

显然∠AOB=45⁰

∴渐近线方程为

又∵顶点A’（0，　　　　 ∴双轴线C的方程　

即

设过A的直线方程为

显然k≠0

由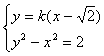

即

若直线与双曲线C交于M（

则

即　　 ∴

此时

∴

这样直线存在，方程为

21．解（1）∵

∴

∴

（2）∵m<n　　　 ∴0<m-a<n-a

又∵

∴0<a<1

又∵

可证在上是增函数

∴在[m．n]上减函数　 ∴

由题意得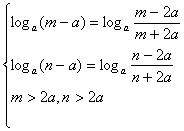

∴

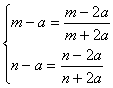
∴方程有两不相等的根

即方程上有两个不等实根

即

上有两个不等实根

令

∴　　　 ∴

∴

 

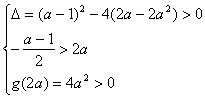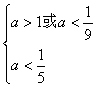
22．解:（1）由 　∴m=3

a₁==1

而展开式第二项

∴a_n=x^n－1

（2）当x=1时，S_n=n

∴

而

　

　

当x≠1时，

 

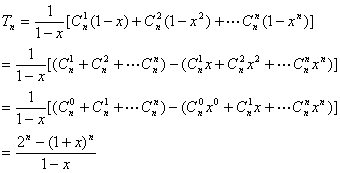
（3）当x>1时，

若，则1+x=3 ,　∴x=2