数学高考模拟试卷
班级 序号 姓名
一、选择题:(本大题共12小题,每小题5分,共60分)
1.已知集合![]() 若
若![]() ,则B的个数为 ( )
,则B的个数为 ( )
(A)3个 (B)4个 (C)8个 (D)16个
2.已知等差数列![]() 中,
中,![]() ,则
,则![]() 的值为 ( )
的值为 ( )
(A)![]() (B)5 (C)20 (D)25
(B)5 (C)20 (D)25
3.不等式![]() 的解集是 ( )
的解集是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4.定义运算![]() 为:
为:![]() ,例如
,例如![]() ,
,
则![]() 的取值范围是 ( )
的取值范围是 ( )
(A)(0,1) (B)![]() (C)
(C)![]() (D)
(D)![]()
5.设平面上有四个互异的点A、B、C、D,若![]() 则
则![]() 的形状是 ( )
的形状是 ( )
(A)直角三角形 (B)等腰三角形
(C)等腰直角三角形 (D)等边三角形
6.若![]() 则
则![]() 的最小值是 ( )
的最小值是 ( )
(A)5 (B)4 (C)3 (D)2
7.若![]() 的内角满足
的内角满足![]() ,
,
则角A的取值范围是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8.若![]() ,则函数
,则函数![]() 的最小值为 ( )
的最小值为 ( )
(A)![]() (B)0 (C)2 (D)4
(B)0 (C)2 (D)4
9.已知![]() 是首项为1,公比为2的等比数列,
是首项为1,公比为2的等比数列,
则![]() 等于 ( )
等于 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.若![]() ,则
,则![]() 的值域是 ( )
的值域是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
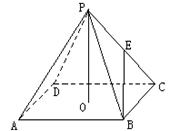 11.已知正四棱锥P-ABCD的高和底面边长均为
11.已知正四棱锥P-ABCD的高和底面边长均为![]() ,
,
E是侧棱PC的中点,则PA与BE所成的角为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
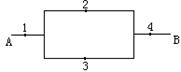 12.如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有 ( )
12.如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有 ( )
(A)10 (B)12
(C)13 (D)15
二、填空题:(本大题共4小题,每小题4分,共16分)
13.函数![]() 的单调增区间是 。
的单调增区间是 。
14.函数![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() ,则
,则![]() = 。
= 。
15.过抛物线![]() 焦点的直线交抛物线于A、B两点,若
焦点的直线交抛物线于A、B两点,若![]() ,O为坐标原点,则
,O为坐标原点,则![]() 的重心的横坐标为 。
的重心的横坐标为 。
16.若![]() 在椭圆
在椭圆![]() 上运动,则
上运动,则![]() 的最大值是 。
的最大值是 。
三、解答题:
17.(本题满分12分)
解关于![]() 的不等式:
的不等式:![]()
![]()
18.(本题满分12分)
已知A、B、C是三角形的内角,向量![]() ,且
,且![]() ,其中
,其中![]() =(1,0),
=(1,0),![]() =(0,1),(1)求证:
=(0,1),(1)求证:![]() ;
;
(2)若![]() ,
,![]() 的最大边为
的最大边为![]() ,求
,求![]() 的面积。
的面积。
19.(本题满分12分)
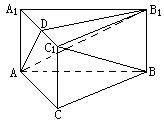
如图,正三棱柱![]() 中,D是
中,D是![]() 的中点,
的中点,
(1)求证:![]() ;(2)求证:
;(2)求证:![]() ;
;
(3)若![]() ,①求直线
,①求直线![]() 与
与![]() 所成的角的正切值;②求
所成的角的正切值;②求![]() 到平面
到平面![]() 的距离。
的距离。
20.本题满分12分)
某届世界杯乒乓球赛中,1号种子选手与2 号种子选手在决赛中相遇,每局比赛中1号种子选手获胜的概率都是0.6,每局比赛相互独立,比赛采用五局三胜制,(1)1号种子选手以总比分3∶1获胜的概率是多少?(2)2号种子选手夺冠 的概率是多少?(3)若比赛改为七局四胜制,2号种选手夺冠的可能性变大还是变小?说明理由。(精确到0.001)
21.(本题满分12分)
已知两点M(-2,0),N(2,0),动点P在y轴上的射影为H,若![]() ,
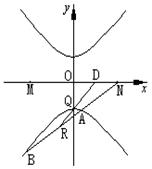
,![]() 分别是公比为2的等比数列的第三,四项,(1)求动点P的轨迹方程C;(2)已知过点N的直线
分别是公比为2的等比数列的第三,四项,(1)求动点P的轨迹方程C;(2)已知过点N的直线![]() 交曲线C于x轴下方两个不同的点A、B,设AB的中点为R,若过R与定点
交曲线C于x轴下方两个不同的点A、B,设AB的中点为R,若过R与定点![]() 的直线交
的直线交![]() 轴于点D(
轴于点D(![]() ,0),求
,0),求![]() 的取值范围。
的取值范围。
22.(本题满分14分)
已知![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,且方程
上是减函数,且方程![]() 有三个根,它们分别为
有三个根,它们分别为![]() 。 (1)求
。 (1)求![]() 的值; (2)求证:
的值; (2)求证:![]() ;
;
(3)求![]() 的取值范围。
的取值范围。
数学高考模拟试卷参考答案
一、选择题:CCBCB BCDAD AC
二、填空题:13.![]() ,14. 2 15.2 16.
,14. 2 15.2 16.![]()
三、解答题:17.解:原不等式等价于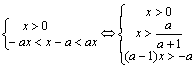
①![]() ;②
;②![]()
18.解:(1)∵![]() ∴
∴![]() ∴
∴![]()
∴![]() ∴
∴![]() ∴
∴![]()
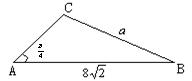 (2)解 ∵
(2)解 ∵![]() ∴
∴![]() ,
,
![]()
∴C为最大角,![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]() ∴
∴![]() ∵
∵![]()
∴![]() ∴
∴![]()
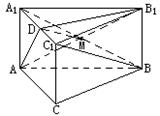 19. (1)证明:连
19. (1)证明:连![]() 与
与![]() 交于点
交于点![]() ,连
,连![]() ,
,
∵![]() 为矩形,∴
为矩形,∴![]() 为
为![]() 的中点,∵
的中点,∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ∵
∵![]() ,
,
![]() ,∴
,∴![]()
(2)正三棱柱![]() 中,
中,![]() 为正三角形,D为
为正三角形,D为![]() 的中点,∴
的中点,∴![]() ,又
,又![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
∴![]()
![]()
(3) ①![]() ∴
∴![]() 即为直线
即为直线![]() 与
与![]() 所成的角,
所成的角,
在![]() 中,
中,![]() 在
在![]() 中,
中,![]() ,∴
,∴![]()
∴直线![]() 与
与![]() 所成的角的正切值为
所成的角的正切值为![]() 。
。
②∵![]() ,∴
,∴![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,设为
的距离,设为![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
20.解(1)设“1号种子选手以总比分3∶1获胜”为事件A,
![]()
(2)设“2号种子选手夺冠”为事件B,则2号以3∶0获胜的概率为![]() ;2号以3∶1获胜的概率为
;2号以3∶1获胜的概率为![]() ,2号以3∶2获胜的概率为
,2号以3∶2获胜的概率为![]() ,
,
∴![]()
(3)比赛改为七局四胜制后,2号种子选手夺冠的概率为
![]()
∵0.290<0.317,∴2号种子选手夺冠的可能性变小了。
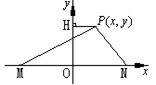 21.解:(1)设
21.解:(1)设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,由题意知:
,由题意知:![]() ,
,
 即
即![]() 为所求。
为所求。
(2)设![]() ,代入
,代入![]() 得
得
![]() ,依题意有
,依题意有
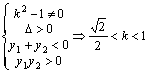
AB的中点坐标![]() ,RQ方程:
,RQ方程:![]() ,令
,令![]() ,得
,得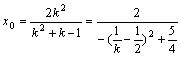 ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() 。
。
22.解:(1)![]() ,∵
,∵![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
∴![]() ,即
,即![]() ,从而
,从而![]()
(2)![]() ,又
,又![]() ,∴
,∴![]() 从而
从而![]() ,由于
,由于![]() ,
,
∴![]() ,
,![]() 的两根为
的两根为![]() ,由题设
,由题设![]() ,
,
即![]() ,∴
,∴![]() ,
,![]()
(3) ∵![]() 是
是![]() 的三个根,∴
的三个根,∴![]()
![]() ,于是
,于是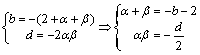
![]() ,∵
,∵![]() ,∴
,∴![]()