数学高考模拟试题
一、选择题(每小题5分,共60分)
1.设全集U=R,集合![]() ,集合
,集合![]() ,则集合
,则集合![]() 为( ).
为( ).
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() D.
D.![]()
2.在下列函数中,值域是(0,+∞)的函数是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知直线![]() 与圆
与圆![]() 无公共点,则点
无公共点,则点![]() 一定( ).
一定( ).
A.在圆内 B.在圆外 C.在圆上 D.都有可能
4.若![]() ,
,![]() ,
,![]() 的值是( ).
的值是( ).
A.![]() B.
B.![]() C.-3 D.3
C.-3 D.3
5.函数![]() ,且
,且![]() 的图象为( ).
的图象为( ).
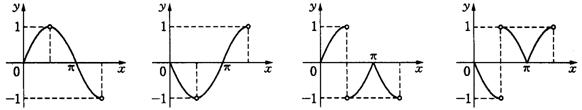
A B C D
6.等差数列![]() 与等比数列
与等比数列![]() 满足:
满足:![]() ,
,![]() ,则
,则![]() 与
与![]() 的大小关系是( ).
的大小关系是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.直线l是双曲线![]() 的右准线,以原点为圆心且过双曲线的焦点的圆被直线l分成弧长为2比1的两段圆弧,则该双曲线的离心率是( )
的右准线,以原点为圆心且过双曲线的焦点的圆被直线l分成弧长为2比1的两段圆弧,则该双曲线的离心率是( )![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设函数f(x)的定义域为R,最小正周期为![]() ,若
,若![]()
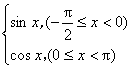
则![]() 的值为( )
的值为( )![]()
 A.0 B.1 C.
A.0 B.1 C.![]() D.
D.![]()
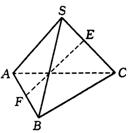
9.如图,在正四面体S-ABC中,E、F分别是SC、AB的中点,则直线EF与SA所成的角为( ).
A.90° B.60° C.45° D.30°
10.定义在实数集R上的偶函数![]() 满足
满足![]() ,且在区间
,且在区间![]() ,
,![]() 上单调递增,设
上单调递增,设![]() ,
,![]() ,则a、b、c的大小关系是( )
,则a、b、c的大小关系是( )![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.对于函数![]() ,作
,作![]() 的代换,则总不改变函数
的代换,则总不改变函数![]() 的值域的代换是( ).
的值域的代换是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.在轴截面为直角三角形的圆锥内有一个内接圆柱,已知此圆柱的全面积等于该圆锥的侧面积,则该圆锥顶点到圆柱上底面的距离是圆锥母线长的( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分,共16分)
13.如果抛物线![]() 的准线方程是x=-3,那么这条抛物线的焦点坐标是________.
的准线方程是x=-3,那么这条抛物线的焦点坐标是________.
14.圆锥轴截面的顶角为120°,过顶点的截面三角表面积的最大值为2,则圆锥的侧面积是________.
15.从1到10这10个自然数中任取3个互不相邻的自然数的取法总数是________.
16.某工厂产值连续三年持续增长,已知年平均增长率P,若这三年的增长率分别为![]() 、
、![]() 、
、![]() ,则
,则![]() 的最小值是________.
的最小值是________.
三、解答题(第17~21题每题12分,第22题14分,共74分)
17.已知集合![]() ,集合
,集合![]() ,求集合
,求集合![]()
18.在三角形ABC中,角A、B、C的对边分别是a、b、c,若a+b=10,![]() ,
,
(1)求证:![]() 不大于120°;
不大于120°;
(2)若△![]() 外接圆的直径为10,求
外接圆的直径为10,求![]() 的值
的值![]()
19.已知线段![]() 矩形ABCD所在的平面,M、N分别是AB、PC的中点.
矩形ABCD所在的平面,M、N分别是AB、PC的中点.
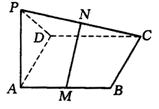
(1)求证:MN∥平面PAD;
(2)当二面角A-CD-P为45°时,求证:MN⊥平面PCD;
(3)在满足(2)的条件下,若AB=4,AD=2,求四棱锥N-ABCD的体积.
20.有一个湖泊,上游一河道每天向该湖流入![]() 的水,流入的水中含有某种不能自然分解的污染物质.与该湖联通的另一河道每天向下游流出的水也是
的水,流入的水中含有某种不能自然分解的污染物质.与该湖联通的另一河道每天向下游流出的水也是![]() ,湖水始终保持在200万
,湖水始终保持在200万![]() .现假设湖水蒸发和下雨恰好平衡,该污染物与湖水能均匀混合,并测得湖水中该污染物的浓度已达到0.2克/
.现假设湖水蒸发和下雨恰好平衡,该污染物与湖水能均匀混合,并测得湖水中该污染物的浓度已达到0.2克/![]() .后来,由于上游治理了污染源,流入湖中的水已不再含有该污染物.
.后来,由于上游治理了污染源,流入湖中的水已不再含有该污染物.
(1)试求上游污染中止后n天,湖水中该污染物的浓度;
(2)欲使湖水该污染物的浓度不超过0.05克/![]() 的标准,若不采取其他治污措施,湖水需要多少天才能达标?(
的标准,若不采取其他治污措施,湖水需要多少天才能达标?(![]() ,
,![]()
21.已知椭圆![]() 的焦距为2c,左准线为l,长轴顶点为
的焦距为2c,左准线为l,长轴顶点为![]() 、
、![]() ,过椭圆上任意纵坐标非零的点P作直线
,过椭圆上任意纵坐标非零的点P作直线![]() 与
与![]() 分别交l于M、N两点
分别交l于M、N两点![]()
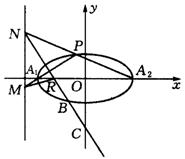
(1)试问在线段![]() (O为原点)上是否能找到一点Q,使得对于上述的点P,
(O为原点)上是否能找到一点Q,使得对于上述的点P,![]() 恒为直角,若能,求出点Q的坐标;若不能说明理由;
恒为直角,若能,求出点Q的坐标;若不能说明理由;
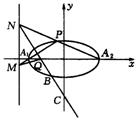
(2)如图,设直线NR与椭圆交于点B,与y轴交于点C,当直线PN的斜率为![]() 时,点B恰为线段RC的中点,求此椭圆的离心率.
时,点B恰为线段RC的中点,求此椭圆的离心率.
22.已知二次函数![]() R)满足
R)满足![]() ,对任意实数x,都有
,对任意实数x,都有![]() ,且
,且![]() 时,总有
时,总有![]() .
.
(1)求![]() ;
;
(2)求a,b,c的值;
(3)当![]() ,
,![]() 时,函数
时,函数![]() (m
(m![]() R)是单调函数,求m的取值范围.
R)是单调函数,求m的取值范围.
参考答案
1.C 2.D 3.A 4.A 5.C 6.C 7.D 8.D 9.C 10.D
11.B 12.C 13.(1,0) 14.![]() 15.
15.![]() =56 16.3P
=56 16.3P
17.![]() ,或
,或![]() ,又
,又![]()
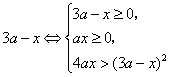 或
或![]()
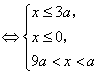 或
或![]() (以上a<0)
(以上a<0)![]() 或
或
![]() ,所以
,所以![]() ;
;![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]()
18.(1)由余弦定理:![]()
![]() ,由已知a+b=10,
,由已知a+b=10,![]() ,ab≤25,则
,ab≤25,则![]() ,
,![]() ,因为0°<C<180°,所以C≤120°,即
,因为0°<C<180°,所以C≤120°,即![]() 不大于120°.
不大于120°.
(2)由正弦定理:![]() =2R=10,得
=2R=10,得![]() ,
,![]() ,C=60°,或C=120°,
,C=60°,或C=120°,![]() ,
,![]() ,
,
当C=60°,A+B=120°,代入得:![]() ,
,![]()
![]() ,当C=120°时,A+B=60°
,当C=120°时,A+B=60° ![]() ,
,![]() ,
,![]()
19.(1)取PD的中点E,连接AE、EN,因为EN ![]()
![]() ,而
,而![]()
![]() AM,所以ANME为平行四边形,MN∥AE.则MN∥平面PAD
AM,所以ANME为平行四边形,MN∥AE.则MN∥平面PAD![]()
(2)![]() 矩形ABCD所在的平面,故
矩形ABCD所在的平面,故![]() ,又ABCD为矩形,则
,又ABCD为矩形,则![]()
![]() 所以
所以![]() 平面PAD,
平面PAD,![]() ,AE∥MN,
,AE∥MN,![]() ,因为
,因为![]() ,
,![]() ,则
,则![]() 是二面角A-CD-P的平面角,
是二面角A-CD-P的平面角,![]() =45°,△
=45°,△![]() 为等腰直角三角形,又E是斜边PD的中点,
为等腰直角三角形,又E是斜边PD的中点,![]() ,则
,则![]() ,已证
,已证![]() ,可得
,可得![]() 平面PCD.
平面PCD.
(3)连AC,取AC中点O,连ON,则ON∥PA,且![]() ,又PA=AD=2,则ON=1,
,又PA=AD=2,则ON=1,![]() 平面ABCD,故
平面ABCD,故![]() 平面ABCD,即NO为四棱锥N-ABCD的高,
平面ABCD,即NO为四棱锥N-ABCD的高,![]()
20.(1)上游污染中止n天后,湖水中污染物浓度为![]() ,则可建立关系式:
,则可建立关系式:![]() ,则
,则![]() ,又
,又![]() =0.2克/
=0.2克/![]() ,所以
,所以![]()
![]()
![]()
(2)设![]() ,即0
,即0![]() 2×
2×![]() ,则
,则![]()
![]() (天)
(天)
21.(1)当点P运动到特殊位置(0,b)时,直线![]() 的方程为bx+ay=ab,求得
的方程为bx+ay=ab,求得![]()
![]()
![]() ,同法求得
,同法求得![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,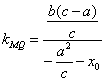 ,
,
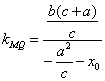 由
由![]() 解得
解得![]() ,推测:椭圆的左焦点F(-c,0)满足条件.证明:设椭圆上任意一点
,推测:椭圆的左焦点F(-c,0)满足条件.证明:设椭圆上任意一点![]() ,
,![]() 椭圆的左焦点为F(-c,0),则直线
椭圆的左焦点为F(-c,0),则直线![]() 的方程为:
的方程为:![]() ,令
,令![]() ,求得点N的坐标为
,求得点N的坐标为![]() ,
,![]() ,又直线
,又直线![]() 的方程为:
的方程为:![]() ,令
,令![]() ,求得点M的坐标为
,求得点M的坐标为![]() ,
,![]() ,则直线MF的斜率
,则直线MF的斜率![]() ,直线NF的斜率
,直线NF的斜率![]() ,
,![]()
![]()
![]() .因为点
.因为点![]() ,
,![]() 在椭圆上,则
在椭圆上,则![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() 恒为直角(Q与F重合).
恒为直角(Q与F重合).
(2)直线![]() 的方程为
的方程为![]() ,求得
,求得![]() ,
,![]() ,且Q与F重合.直线BN的斜率
,且Q与F重合.直线BN的斜率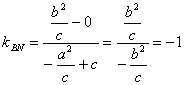 ,所以直线BN的方程为
,所以直线BN的方程为![]() ,点C的坐标为(0,-c),因为B是CF中点,则点B的坐标是
,点C的坐标为(0,-c),因为B是CF中点,则点B的坐标是![]() ,
,![]() ,把点B的坐标代入到椭圆方程中得:
,把点B的坐标代入到椭圆方程中得:![]() 1,即
1,即![]() ,整理得:
,整理得:![]() ,
,![]() ,或
,或![]() (舍去),所以
(舍去),所以![]()
22.(1)![]() 对任意实数x,都有
对任意实数x,都有![]() ,所以
,所以![]() ,又
,又![]() 在
在![]() 时,有
时,有![]() ,故
,故![]() ,因此有
,因此有![]() .
.
(2)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,因为
,因为![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时取等号).又因为对任意实数x,都有
时取等号).又因为对任意实数x,都有![]() ,所以
,所以![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立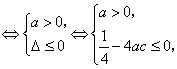 故
故![]() 且
且![]() ,因此有
,因此有![]() ,从而
,从而![]()
![]()
(3)![]()
![]()
![]() ,
,![]() 的对称轴是
的对称轴是![]() ,因为
,因为![]() (m
(m![]() R)在
R)在![]() ,
,![]() 上是单调函数,所以
上是单调函数,所以![]() 或
或![]()