数学奥林匹克高中训练题（27）
第一试
一、选择题（本题满分36分，每小题6分）
1．(训练题57)若
是
上的减函数，且图像经过点
和点
，则不等式
的解集为(D)．
(A)
(B)
(C)
(D) 
2．(训练题57)若函数
的图像关于直线
对称，则
的值等于(C)．
(A)
或
(B)
或
(C)或
(D)或
3．(训练题57)设椭圆的方程为
为短轴的一个端点，
为椭圆上相异两点，若总存在以
为底边的等腰
，则直线的斜率
的取值范围是(C)．
(A)
(B)
(C)
(D)
4．(训练题57)是定义在上的函数，且对任意的
满足
．已知当
时，
．那么，当
时，的表达式为(C)．
(A)
(B)
(C)
(D)
5．(训练题57)已知
是边长为１的正方体，
为线段
上的动点，
为底面
上动点．则
的最小值为(A)．
(A)
(B)
(C)
(D)
6．(训练题57)已知在数列
中，
为前
项的和，且满足
．则
的表达式为(D)．
(A)
(B)
(C)
(D)
二、填空题（本题满分54分，每小题9分）
1．(训练题57)在
中，
于
，且
．则
的最大值为 
．
2．(训练题57)已知函数
的反函数图像关于点
成中心对称．则实数的值 3 ．
3．(训练题57)集合
，当
时，的取值范围为 
．
4．(训练题57)已知线段
平面
，且到平面的距离等于８，点
是平面内的一动点，且满足
．若
，则点与距离的最小值为 17 ．
5．(训练题57)已知多项式
整除多项式
．则实数
3 ，
．
6．(训练题57)设
，其中
表示不超过
的最大整数。则
值等于 242
．
三、(训练题57)(本题满分20分)已知的三内角平分线分别为
．若向量
满足关系
，试证：为正三角形．
四、(训练题57)(本题满分20分)已知数列
表示其前项和．若满足关系
，求数列的通项公式的表达式．(
)
五、(训练题57)(本题满分20分)已知椭圆的半长轴为，半短轴为
，短轴的一个端点为
，
为椭圆上异于点的任意两点，
．若点在线段
上的身影为
，试求点的轨迹．
第二试
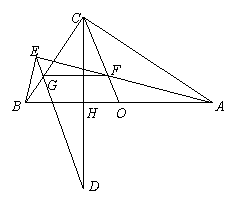
一、(训练题57)(本题满分50分)如图，已知在
中，
为斜边
的中点，
为斜边上的高，延长到，使得
为中线
上任意一点，过作
的延长线于
，连结
交
于
．求证：
．
二、(训练题57)(本题满分50分)设
．求函数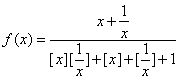
的值域．其中
表示不超过的最大整数．
三、(训练题57)(本题满分50分)圆周上分布着
个点，现将它们任意地染成白色或黑色，如果从某一点开始，依任一方向绕圆周运动到任一点，所经过的（包括该点本身白点总数恒大于黑点总数，则称该点为好点．为确保圆周上至少有一个好点．试求所染黑点数目的最大值．
 |