数学奥林匹克高中训练题（29）
第一试
一、选择题（本题满分36分，每小题6分）
1．(训练题39)若
是空集，对于一特殊集合
来说，下列命题：⑴
，⑵
，⑶
，⑷ 
中正确的个数为 (D)．
(A)
(B)
(C)
(D)
2．(训练题39)已知函数
，
，则
的值是(B)．
(A)
(B) (C)
(D)与
的值无关
3．(训练题39)计算：
(B)．
(A)
(B)
(C)
(D)
4．(训练题39)已知
，则多项式
除以
后，所的余式为(A)．
(A)
(B) (C)
(D)
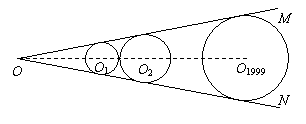5．(训练题39)如图，有
个圆分别与
的两边都相切，而这些圆依次一个相切于另一个，如果最大圆与最小圆的半径分别为
．那么，它们中的正中间的圆的半径为(C)．
(A)
(B)
(C)
(D)不能确定
 |
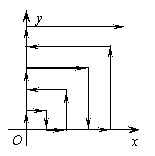6．(训练题39)如图，一个粒子在第一象限运动，在第一秒内它从原点运动到
，尔后它接着按图所示在与
轴，
轴的平行方向上来回运动，且每一
秒移动一个单位长度，那么，秒后，这个粒子所在位置为(D)．
(A)
(B)
(C)
(D)
二、填空题（本题满分54分，每小题9分）
1．(训练题39)计算：
．
2．(训练题39)
除以
，余数是
．
3．(训练题39)已知
，
，
，则的值为 
．
4．(训练题39)设任意实数
，要使
恒成立，则
的最小值是 9 ．
5．(训练题39)已知两点
，
．若有一整点
（注：横，纵坐标均为整数的点称为整点），使得
的面积最小，则的面积的最小值为 1 ．
6．(训练题39)已知平面直角坐标系中有两动点
，
，其中
为任意实数，则
之间的最小距离为 
．
三、(训练题39)(本题满分20分)已知正数数列
满足
且
，
．求的通项公式．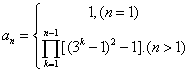
四、(训练题39)(本题满分20分)能被
整除的个不同的正偶数与能被整除的
个不同的正奇数的总和为
．对于所有这样的
，
的最大值为
．问的最大值为多少？请证明你的结论．（1998）
五、(训练题39)(本题满分20分)已知
，且
．
求证：
．
第二试
一、(训练题39)(本题满分50分)在不超过
的自然数中，任意选取
个数，则这个数中一定存在两数，其差为或或
．
二、(训练题39)(本题满分50分)已知距离为
的
两点在直线
的同侧，且到直线的距离分别为
．问能否作出经过两点且与直线相切的圆？若能，请写出作法，画图并求出圆的半径，若不能，说明理由．
三、(训练题39)(本题满分50分)若百分位数字为
的位自然数
的各位数字之和为，其中
，当
的值最小时，是多少？（1999）