数学奥林匹克高中训练题（30）
第一试
一、选择题（本题满分36分，每小题6分）
1．(训练题37)
是由
个
组成的位数，
是由个
组成的位数，则
的各位数字之和为(C)．
(A)
(B)
(C)
(D)
2．(训练题37)已知
，则方程
的所有根的和为(C)．
(A)
(B)
(C)
(D)
3．(训练题37)已知三个正数、、
之和为10，如果它们之中没有一个大于其余数的
倍，那么
的最小值是(B)．
(A)
(B)
(C)
(D)
4．(训练题37)已知
，
为正整数，则
的个位数字为(B)．
(A)
(B) (C)
(D)
5．(训练题37)已知
中，
成等差数列，则
的取值范围是(B)．
(A)
(B)
(C)
(D)
6．(训练题37)一只小球放入一长方形容器内，且与共点的三个面相接触，小球上有一点到这三个面的距离分别是
，，
，则这只小球的半径(D)．
(A)只为 (B)只为 (C)只为
(D)以上说法不对
二、填空题（本题满分54分，每小题9分）
1．(训练题37)已知
，则正整数
的最大值为
55
．
2．(训练题37)已知
是正的内切圆，
与外切且与的两边相切，…，
与
外切且与两边相切．那么，在内所有这些可能的圆（包括，）的面积之和与的面积之比为
．
3．(训练题37)
是边长为的正所在平面上的一动点，且
，则动点 的轨迹为 以正的中心为圆心，2为半径的圆
．
4．(训练题37)已知方程
有
组正整数解
．那么的最大值是 304 ．
5．(训练题37)已知正四面体
的六条棱的长分别为
，
，
，
，
，
。则
的最小值为 8 ．
6．(训练题37)已知对于每一个实数
和
，函数
满足
．若
，则满足
的正整数对
共有
16
个．
三、(训练题37)(本题满分20分)已知不等式组
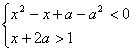的整数解恰好有两个，求的取值范围？（
）
四、(训练题37)(本题满分20分)当为何实数时，
有最小值，最大值是多少？
五、(训练题37)(本题满分20分)已知函数在
上有定义，且满足下列条件：①在严格递减，且
；②在上恒有
．
求函数值
；（2）
给出一个满足提设条件的函数．
第二试
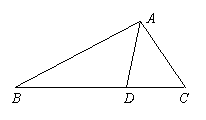一、(训练题37)(本题满分50分)已知如图，
是锐角的角平分线，
，
，且
．求证
．
二、(训练题37)(本题满分50分)求
的末四位数．（4688）
三、(训练题37)(本题满分50分)已知是正整数，
是正奇数，
是正常数，且
，函数
．若实数
满足
求证：
．