数学奥林匹克高中训练题（31）
第一试
一、选择题（本题满分36分，每小题6分）
1．(训练题31)方程
实根的个数是(B)．
(A)0 (B)1 (C)2 (D) 无穷多
2．(训练题31)已知正方体
的棱长为1，点
关于直线
、
的对称点分别为
、
，则、两点间的距离是(A)．
(A) 
(B) 
(C) 
(D) 
3．(训练题31)已知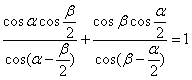
．则
的值等于(A)．
(A) 1
(B) 
(C) 
(D) 
4．(训练题31)设
．则
的展开式是(C)．
(A)
(B)
(C)
(D)
5．(训练题31)在圆
内，过点
恰有
条弦的长度成等差数列．如果公差
，那么，取值的集合是(D)．
(A){4，5，6} (B){6，7，8，9} (C){3，4，5} (D){3，4，5，6}
6．(训练题31)给定平面内的五个点
任意三点不共线，由这些点连成4条线段，每个点至少是一条线段的端点，则不同的连结方式有(D)．
(A)120种 (B)125种 (C)130种 (D)135种
二、填空题（本题满分54分，每小题9分）
1．(训练题31)函数
的递增区间是
．
2．(训练题31)已知四面体
的体积为
，
为棱
的中点，延长
到
，使
，设过
三点的平面交
于
，则四面体
的体积是
．
3．(训练题31)满足
的锐角
= 
．
4．(训练题31)设
是集合
的含有3个元素的所有子集的元素之和，且
．则极坐标方程
表示的曲线是 
，双曲线的右支 ．
5．(训练题31)已知A、B、C是平面上任意三点，且
．则
的最小值是
．
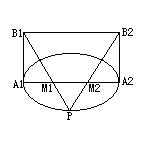6．(训练题31)如图，有矩形
中，已知
．以边
为长轴作椭圆
，的短轴长等于
．在上任取一点（不同于长、短轴的端点）．设直线
于的交点分别为
．则
．
三、(训练题31)(本题满分20分)设为正整数．求证：
．
四、(训练题31)(本题满分20分)在数列
中，
．求
的表达式．
五、(训练题31)(本题满分20分)经过点
作抛物线
的四条弦
，且
四点的纵坐标成等差数列．求证：
．
第二试
一、(训练题31)(本题满分50分)设
为
斜边上的高，
分别是
的内心。求证：
的外接圆半径与
的内切圆半径相等．
二、(训练题31)(本题满分50分)设
和
分别表示整数
的最大公约数和最小公倍数．求满足
的所有整正数解．
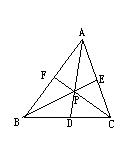
三、(训练题31)(本题满分50分)如图，的三条内线段
交于点．用红、兰两种颜色对的三条边线和三条内线段染色，是同色的三线不交于一点．证明：在途中所有的三角形中，至少存在两个同色三角形,且它的各边或延长线被另一线截得的两线段之比的和大于3．