数学奥林匹克高中训练题（33）
第一试
一、选择题（本题满分36分，每小题6分）
1．(训练题33)方程
的解集是(D)．
(A)
(B)
(C)
(D)
2．(训练题33)一个三角形的三条边恰为
，则这个三角形中最大角为(B)．
(A)
(B)
(C)
(D)
3．(训练题33)己知
是
上的奇函数,
是上的偶函数 , 若
, 则
(A)．
(A)
(B)
(C)
(D)
4．(训练题33)满足方程组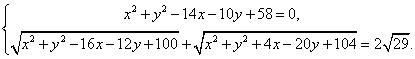
的数组
是(C)．
(A) 
(B)
(C) 
(D) 
5．(训练题33)
是
的(A)．
(A)必要条件, 但非充分条件． (B)充分条件, 但非必要条件．
(C)充分条件, 也是必要条件． (D)非充分条件, 也非必要条件．
6．(训练题33)正方形纸片
, 沿对角线
对折, 使
点在面
外, 这时
与面所成的角一定不等于(D)．
(A)30° (B)45° (C)60° (D)90°
二、填空题（本题满分54分，每小题9分）
1．(训练题33)若
, 则 
4 ．
2．(训练题33)
，则
．
3．(训练题33)若
，则
1 ．
4．(训练题33)多项式
展开后合并同类项，所得结果中
的奇次项系数之和为 -1 ．
5．(训练题33)正方体
棱长为1，
是
中点，
是
中点，则四面体
的体积是 
．
6．(训练题33)在坐标平面上，由条件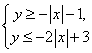
所限定的平面区域的面积是 16 ．
三、(训练题33)(本题满分20分)
是有理数还是无理数？请证明！
四、(训练题33)(本题满分20分)公差为4的有限项的等差数列，它的首项的平方与其余所有项之和不超过100．请你回答，这个等差数列最多可以有多少项？（8）
五、(训练题33)(本题满分20分)
均为实数，
．证明：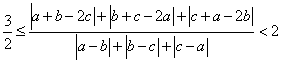
．
第二试
一、(训练题33)(本题满分50分)
分别是锐角
的外心与垂心，点在
上，
，点在上，
．证明：
．
二、(训练题33)(本题满分50分)某工厂的
位工人共提了
条
不同的合理化建议．经统计发现，每两个工人提的合理化建议中都至少有一条相同的建议，但没有两个工人所提的建议完全相同．证明：
．
三、(训练题33)(本题满分50分)在圆上有21个点．证明：以这些点为端点组成的所有弧中，不超过
的弧不少于100条．