数学奥林匹克高中训练题(34)及答案

数学奥林匹克高中训练题（34）

第一试

一、选择题（本题满分36分，每小题6分）

1．(训练题34)对于一切实数x，所有的二次函数f(x)=ax²+bx+c(a＜b)的值恒为非负实数. 则的最小值是(D)．

(A)　　   (B)　　  　(C)2　　　　(D)3

2．(训练题34)已知曲线y²=ax与其关于点（1，1）对称的曲线有两个不同的交点. 如果过这两个交点的直线的倾斜角为45°，那么实数a的值是(A)．

(A)2　　　　 (B)4　　　　 (C)　　　　　　 (D)

3．(训练题34)已知△ABC的三边长a、b、c满足关系式a²－a－2b－2c=0，a+2b－2c+3=0. 则△ABC最大内角的度数是(B)．

(A)150°　　 (B)120°　　 (C)90°　　　　　(D)60°

4．(训练题34)设f(x)=x⁴+ax³+bx²+cx+d，其中a、b、c、d为常数. 如果f(1)=1，f(2)=2，f(3)=3，那么的值是(C)．

(A)1　　　　 (B)4　　　　  (C)7　　　　　　 (D)8

5．(训练题34)设函数且的最小值为a_n，最大值为b_n，记c_n=(1－a_n)(1－b_n). 则数列{c_n} (C)．

(A)是公差不为零的等差数列　　　　　　  (B)是公比不为1的等比数列　

(C)是常数列　　　　　　　　　　　　　　 (D)不是等差数列也不是等比数列

6．(训练题34)设M是集合S={1，2，3，…，1998}的子集，且M中每一个正整数（元素）仅含有一个0. 则集合M所含元素最多有(D)．

(A)324个　　　　(B)243个　　　　　　  (C)495个　　　　　　  (D)414个

二、填空题（本题满分54分，每小题9分）

1．(训练题34)已知关于x的实系数方程x²－2x+2=0和x²+2mx+1=0的四个不同的根在复平面内对应的点共圆，则m取值的集合是　   ．

2．(训练题34)已知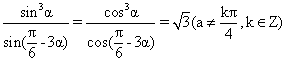. 则tan2α的值是　　 ．

3．(训练题34)自椭圆的中心作两条互相垂直的弦AC和BD，顺次连结A、B、C、D得一四边形. 那么四边形ABCD面积S的最大值是　 12 　　．

4．(训练题34)设正数数列{a_n}的前n项和为S_n，且存在正数t，使得对于所有的正整数n有成立. 如果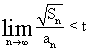，那么t的取值范围是　　　 ．

5．(训练题34)已知球内接四棱锥S—ABCD的底面是矩形ABCD，且SA=4，SB=8，SD=7，∠SAC=∠SBC=∠SDC. 则BD的长是　　BD＝9　　 ．

6．(训练题34)已知正整数m、n满足m+n=19. 则关于x的方程cosmx=cosnx在区间[0，π]上的解的个数的最大值是　 　　　　 ．

三、(训练题34)(本题满分20分)复数z₁、z₂、z₃、z₄、z₅满足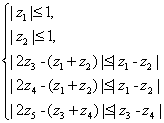，求z₅的最大值．

四、(训练题34)(本题满分20分)设t₁、t₂是方程t²－(5a－2)t－3a²－7a+1=0的两个不等的实根. 求实数a的值，使得对于任何非零实数m，函数是周期函数．

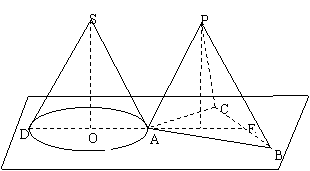
五、(训练题34)(本题满分20分)如图，三棱锥P—ABC的底面ABC与圆锥SO的底面⊙O都在平面α上，且⊙O过点A，又⊙O的直径AD⊥BC，垂足为E. 设三棱锥P—ABC的所有棱长都是1，圆锥的底面直径与母线长也都是1. 求圆锥的顶点S到三棱锥P—ABC的三个侧面的距离．

第二试

一、(训练题34)(本题满分50分)设0＜x₁＜x₂＜…＜x_n＜1.

求证：．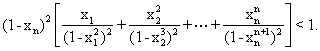

二、(训练题34)(本题满分50分)设凸六边形ABCDEF的六个内角均为钝角，且AB∥DE，BC∥EF，CD∥FA. 以三边AB、CD、EF为边向内各作一个矩形，使它们的顶点两两重合，构成△PQR（如图）.

求证：矩形ABRQ、CDPR、EFQP的面积之比等于sin2C∶sin2E∶sin2A．

三、(训练题34)(本题满分50分)给定平面上n（n≥2）个相异的点．

证明：其中距离为1的点对不超过