数学奥林匹克高中训练题(35)及答案

数学奥林匹克高中训练题（35）

第一试

一、选择题（本题满分36分，每小题6分）

1．(训练题35)b≤1是关于x的不等式acosx+bcos3x＞1没有解的(A)．

(A)必要但不充分条件　　　(B)充分但不必要条件 　

(C)充分必要条件　　　　  (D)不充分也不必要条件

2．(训练题35)三棱锥S—ABC中，SA⊥平面ABC，AB⊥AC，SA=AB，SB=BC，E为SC中点，ED⊥SC交AC于D．则二面角E—DB—C的度数为(C)．

(A)30°　　 (B)45°　　 (C)60°　 　(D)75°

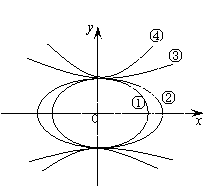3．(训练题35)图中共顶点的椭圆①、②与双曲线③、④的离心率分别为e₁、e₂、e₃、e₄. 其大小关系为(C)．

(A)e₁＜e₂＜e₃＜e₄　　　　(B)e₂＜e₁＜e₃＜e₄　

(C)e₁＜e₂＜e₄＜e₃　　　　(D)e₂＜e₁＜e₄＜e₃

4．(训练题35)设a、b、c∈R⁺. 则的最小值是(D)．

(A)　 (B)　 (C)　 (D)

5．(训练题35)设. 则x、y、z的大小关系是(B)．

(A)x＜y＜z　　　 (B)y＜z＜x　　　 (C)z＜x＜y　　　 (D)z＜y＜x

6．(训练题35)（a，b）表示两正整数a、b的最大公约数. 设(a，b)=1，则(a²+b²，a³+b³)为(C)．

(A)1　　　　　　 (B)2 　　　　　　(C)只能1或2　　　(D)可能大于2

二、填空题（本题满分54分，每小题9分）

1．(训练题35)如果x²－x+2是ax⁹+bx⁸+1的因式，则a=　 　　　　　　．

2．(训练题35)四个城市各派3名政协委员参加k个小组考察活动（每名委员可参加几个小组），规定：①同一城市的委员不在同一组；②不同城市的任意两名委员恰好共同参加一个组活动. 则k的最小值为　  9组　　　．

3．(训练题35)坐标平面上横、纵坐标均为整数的点称为整点. 那么抛物线y=x²+1与直线2x－y+81=0所围成闭区域内（包括边界）的整点个数是　988　　．

4．(训练题35)设则 　　　 ．

5．(训练题35)正有理数a＞1，写成既约分数 则满足pq=30!的正有理数a的个数为　 　512　　　　  ．

6．(训练题35)△ABC中，角A、B、C的对边为a、b、c. 若a²+b²－7c²=0，则　　3　　．

三、(训练题35)(本题满分20分)设实数满足

求的最大值、最小值.．

四、(训练题35)(本题满分20分)已知坐标平面内点A（1，1）与直线l: x=3，动点P到点A的距离为m，到l的距离为n. 若m+n=4, （1）求P点轨迹方程并画出图形；（2）过A作倾角为α的直线s，交轨迹C于Q、R两点，设f(α)=QR.求f(α)表达式及α为何值时，f(α)取最大、最小值.．

五、(训练题35)(本题满分20分)n为正整数，r＞0为实数. 证明：方程xⁿ⁺¹+ rxⁿ－rⁿ⁺¹=0没有模为r的复数根．

第二试

一、(训练题35)(本题满分50分)（1）求正整数x、y，使.（2）有多少个正整数n（n＜1997），能使？（x、y为正整数）．

二、(训练题35)(本题满分50分) 图中⊙O半径为R，⊙O₁的半径为r（R＞r），两圆外切于A，OD切⊙O₁于D，O₁E切⊙O于E，B、C分别为OE、O₁D的中点.（1）证明：B、A、C三点不共线.（2）若R=6，r=3，B为OE的中点，连BA并延长交O₁D于C，求O₁C之长.．

三、(训练题35)(本题满分50分)（1）公路上A、B两镇相距5公里，A、B往外各有两条叉路成　　　形状. 计划在每条叉路上各建一加油站. 要求每个站到A、B镇及到其他站（沿公路经过A、B镇）距离互不相同，且距离均为整数公里，最长不超过15公里，此计划能否实现？（2）若A、B向外各有3条叉路，欲建六个加油站，依然要求站与镇，站与站之间距离互不相同且为整数公里，最长者不超过28公里，能否实现？为什么？．