| 一般数列
(1)数列是按一定次序排列的一列数,定义中的“一列数”是有顺序的,要与数的集合区分开来。数列的通项公式就是定义域为正整数集的函数解析式。
(2)并不是每一个数列都有通项公式,而给出了数列的前n项,写出其通项公式又不一定是唯一的解。
(3)数列前 n项和Sn和通项an之间的关系是:Sn=a1+a2+……+an,其中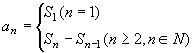
等差、等比数列
(1)如果一个数列从第2项起,后一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。这个常数叫做等差数列的公差;
如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列,这个常数叫做等比数列的公比,用q表示(q≠0)。
等差数列:an=a1+(n-1)d.
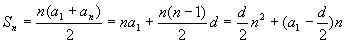 (说明d≠0,Sn是关于n的二次函数)。 (说明d≠0,Sn是关于n的二次函数)。
等比数列:an=a1·qn-1
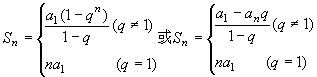
(2) 等差,等比数列的性质 | 等 差 | 等 比 | | ① an=am+(n-m)d (m,n∈N) | ① an=ak·qn-k (n,k∈N) | | ② 若m+n=p+q, 则am+an=ap+aq, (m,n,p,q∈N),反之未必成立 | ② 若m+n=k+l, 则am·an=ak·al(m,n, k,l∈N) | | ③ am+l-al=am+k-ak=md
(其中m,l,k∈N, d为公差) | ③ 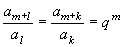 (其中m,l,k∈N) (其中m,l,k∈N) |
特殊数列的求和
特殊数列的求和常用的方法有以下几种:
①直接转化为等差数列或等比数列求和。
②运用倒序相加或错位相减的方法。
③裂项法
④对通项进行分解或组合,将原数列转化成若干个容易求和的数列。(通项展开法)
例1.写出下面数列的一个通项公式,使它的前4项分别是下列各数:
(1)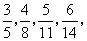 …… ……
(2)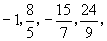 …… ……
(3)0.9,0.99,0.999,0.9999,……
(4)1,0,1,0,……
解:(1)分子依次为3,4,5,6,……,其规律是后续项等于前项加1,又分子首项为3=1+2,故分子的通项为
n+2;分母依次为5,8,11,14,……其规律是后继项等于前项加3,又首项分母为5=3×1+2。故分母的通项为
3n+2。因此,数列的通项公式为: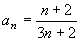 。 。
(2)数列的符号规律是(-1)n.若将第1项看作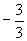 ,如不考虑每一项的符号,则分母为3,5,7,9,……,其通项为2n+1;分子为3,5,7,9,……其通项为(n+1)2-1,将以上规律统一起来,数列的通项公式为: ,如不考虑每一项的符号,则分母为3,5,7,9,……,其通项为2n+1;分子为3,5,7,9,……其通项为(n+1)2-1,将以上规律统一起来,数列的通项公式为:
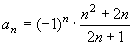 . .
(3)将原数列变形为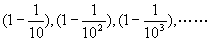 , ,
因此,数列的通项公式为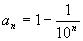 。 。
(4)数列的奇数项为1,可写成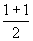 ,偶数项为0,可写成 ,偶数项为0,可写成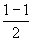 ,因此数列的通项公式为: ,因此数列的通项公式为: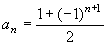 。 。
分析:①在有些情况下,数列的变化规律不易发现,如当本题中数列(1)写成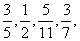 ……时,其项与项数之间的关系不明确,这时就需把数列变形成(1)的形式后才能较明显地看出项与项数之间的关系。 ……时,其项与项数之间的关系不明确,这时就需把数列变形成(1)的形式后才能较明显地看出项与项数之间的关系。
②对于正负号交替的数列,其符号的处理常用(-1)n或(-1)n+1来体现,选取哪一个可由第1项确定。
例2.已知数列1,3a, 5a2,……,(2n-1)an-1, (a≠0). 求此数列前n项的和。
解:设Sn=1+3a+5a2+……+(2n-1)·an-1.......①
则 a·sn=a+3a2+5a3+……+(2n-3)an-1+(2n-1)·an......②
由①-②得:(1-a)·Sn=1+2a+2a2+……+2an-1-(2n-1)·an,
∴ 当a≠1时,
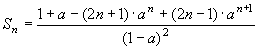 。 。
当a=1时,Sn=1+3+5+……+(2n-1)=n2.
分析:解决数列求和问题,应先观察数列的规律及通项,从而确定具体的求和方法,本题数列的通项
an=(2n-1)·an-1,它可以看作由一个等差数列{2n-1}与一个等比数列{an-1}的对应项相乘所得,这类形式的数列求和时常用错位相减法。
例3.求数列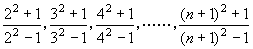 的前n项的和Sn. 的前n项的和Sn.
解:数列的通项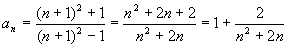 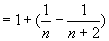 . .
∴ 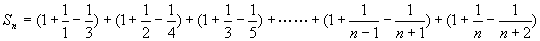
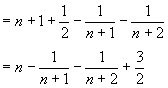
分析:本题采用了裂项法求和。一般地,对于裂项后有明显相消的一类数列,在求和时常用“裂项法”,分式的求和多利用此法。可用待定系数法对通项公式进行拆项,相消时应注意消去项的规律,即消去了哪些项?保留了哪些项?常见的拆项形式有:①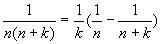 ;②若{an}为等差数列,公差为d,则 ;②若{an}为等差数列,公差为d,则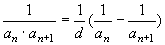 ;③ ;③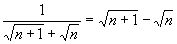 等等。 等等。
例4.已知Sn+an=2n+1,其中Sn是{an}的前n项和,求{an}的通项公式。
解: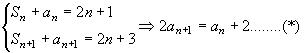
设2(an+1-λ)=an-λ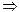 2an+1=an+λ 2an+1=an+λ
由(*) 得:λ=2。
即:2(an+1-2)=an-2.
选代:2(an-2)=an-1-2
……
2(a2-2)=a1-2
∵ 对于任一n∈N, an-2≠0,∴ 各式相乘化简得:2n(an+1-2)=a1-2.
∵ S1+a1=2a1=3 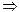 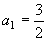 , ∴ , ∴ 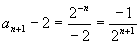 , ,
即: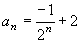 (n∈N). (n∈N).
分析:①首先这是一个关于处理an与Sn关系的一类数列综合题,这类问题经常利用Sn-Sn-1=an(n≥2),消去Sn得{an}的递推式;有时也可以利用这个式子把an代入得Sn的递推式,从而转化为一个递推式问题。
②数列中给出递推公式求通项的方法,一般有以下几种:
Δ直接迭加或迭乘;如给出an+1-an=1.
Δ用待定系数转化成可迭乘的问题,如本题。
Δ用构造新数列的方法解决。如本题中2an+1=an+2. 可两边同时乘以2n,得2n+1·an+1=2n·an+2n+1.
设bn=2n·an, 即二式为bn+1=bn+2n+1于是可用迭加解决。
Δ归纳猜想并用数学归纳法证明的方法。
例5.已知数列{an}是等差数列,且公差d≠0。 {an}中的部分项组成的数列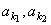 , ,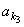 ,……, ,……,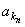 恰为等比数列。且k1=1, k2=5, k3=17. 求 k1+k2+……+kn。 恰为等比数列。且k1=1, k2=5, k3=17. 求 k1+k2+……+kn。
解:由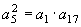 得 得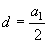 ,q=3。 ,q=3。
∴ 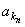 = =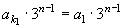 , ,
又∵ 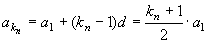 , ,
则:kn=2·3n-1-1.
∴ 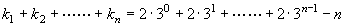
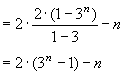
分析:这是一个多数列的问题。且所给的是等比数列与等差数列的相同项问题,我们常从一个入手。去求得另一数列的通项公式。一般地,多数列问题都应注意找到一个数列作为入手点;特别地,当我们处理等差数列与等差数列的相同项问题时,常用整除的想法去解决它。
|