高考第一轮复习数学单元测试卷
数列、极限、数学归纳法
说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），满分150分，考试时间120分钟。
第Ⅰ卷（选择题，共60分）
一、 选择题（本大题共12小题，每小题5分，共60分）
1、
若
构成
A、等差数列 B、等比数列
C、是等差数列也是等比数列 D、不是等差数列也不是等比数列
2、
是等差数列，S10>0，S11<0，则使
<0的最小的n值是
A、5 B、6 C、7 D、8
3、一个等比数列的前n项和为48，前2n项和为60，则前3n项和为
A、183 B、108 C、75 D、63
4、某商品降价10％后欲恢复原价，则应提价
A、10％
B、11％ C、
％
D、12％
5、已知等比数列
的各项均为正数，公比
Q=
，则P与Q的大小关系是
A、P>Q B、P<Q C、P=Q D、无法确定
6、等差数列和
的前n项和分别为Sn和Tn，对一切自然数n都有
，则
等于
B、
C、
D、
7、已知数列的通项公式为
3n-50，则其前n项和Sn的最小值是
A、-784 B、-392 C、-389 D、-368
8、公差不为0的等差数列中，
依次成等比数列，则公比等于
A、
B、
C、2
D、3
9、数列
的前100项的和为
A、
B、
C、 
D、
10、无穷数列
各项的和等于
A、1
B、
C、
D、2
11、是实数构成的等比数列，Sn是其前n项和，则数列
中
A、任一项均不为0 B、必有一项为0
C、至多有有限项为0 D、或无一项为0，或无穷多项为0
12、在数列中，
等于
A0 B1 C、2 D3
第Ⅱ卷（非选择题，共90分）
二、 填空题（本大题共4小题，每小题4分，共16分）
13、等差数列中，
成等比数列，则公差d=_________，公比q=___________。
14、一凸n边形各内角的度数成等差数列，公差是100，最小内角1000，则边数n=_______。
15、一个无穷递减等比数列的首项为1，且每一项都等于它以后所有项的和的k倍，则k的取值范围是________________________。
16、若
，数列的前n项和Sn=5，则n=_________。
三、 解答题（本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。）
17、（本小题满分10分）
数列为等差数列，d是公差，数列
是等比数列，公比为q，又
R，d
R，且
，求公差d和公比q。
18、（本小题满分12分）
数列中，当n为奇数时，
，求这个数列的前2m项的和。
19、（本小题满分12分）
某人向银行贷款2万元用于购房，商定年利率为10％，按复利计算（即本年的利息计入次年的本金生息）。若从借后次年年初开始，每年还4千元，试问，十年时间能否还清贷款？
20、已知
成等差数列，
成等比数列，且
=15，
=14，
=15，
=20。求等差数列的公差d及等比数列
的公比q。
21、（本小题14分）
已知数列1，2，4，…的前n项和
的值。
22、（本小题满分14分）
正项数列，与2的等差中项等于Sn与2的等比中项。
（1）
写出的第三项；
（2）
求的通项公式；
（3）
令
。
高考数学第一轮复习检测
数列参考答案
一、 选择题：（每题5分，共60分）
1、A 2、B 3、D 4、C 5、A 6、B
7、B 8、D 9、A 10、B 11、D 12、C
二、 填空题：（每题4分，共16分
13、
14、8或9 15、
16、35
三、 解答题（共六个小题，满分74分）
17、（10分）
提要：
。
18、（12分）
数列
是公差为10的等差数列，
是公比为2的等比数列，
。
19、（12分）
解、第一年后欠款：
第二年后欠款：
第三年后欠款：
假定10年还清欠款，则
，故得：
[[…[[20000
1.1-4000] 1.1-4000]…] 1.1-4000] 1.1-4000≤0（共含10个4000），两边同除以1.110，可得：
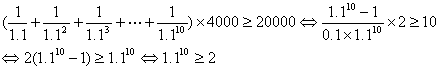
事实上，
所以假定成立，即十年后能还清贷款。
20、（本小题12分）
解：依题意得：
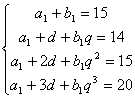，消去
得：
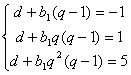
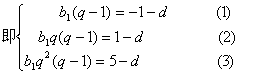
，先解得d=-3，进而得q=2。
21、（14分）
提要：先用待定系数法求出
。
22、(14分)
提要：（1）
。
（2）用递推、归纳、猜想、证明的方法可得到：
。
（3）用裂项相消法求和，从而可求得极限为1。