课时3 数列的极限
一、复习目标
理解数列极限的概念，会判断一些简单数列的极限，了解数列极限的定义，掌握极限的四则运算法则，会求某些数列的极限.
二、例题讲解：
例1．求下列极限：
（1）
；
（2）
；
（3）
；
（4）
解：（4）当
时，原式=
；当
时，则有
所以
原式
，当
时，则有
所以
原式
例2．已知无穷等比数列
的各项和为3，前3项的和为
，求这个数列中所有奇数项的和.
解：设等比数列的公比为
，则
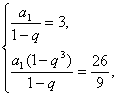解得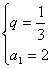
，
等比数列的各奇数项仍成等比数列，其公比为
，故所有奇数项的和为
.
例3．已知数列满足条件：
，且
是公比为
的等比数列，设
求
和
其中
.
解：∵
∴
所以
是首项为
公比为的等比数列，从而
.
当
时，
；
当
时，
；
当
时，
.
所以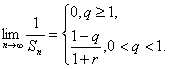
三、同步练习：《高考三人行—学生用书》P337
课时4 函数的极限
一、复习目标
1．熟悉函数极限的概念能正确表述并会推断简单函数的极限.
2．熟悉函数极限的运算、能对函数式变型后推算函数的极限.
二、例题讲解
例1．判断下列函数的极限是否存在：
（1）
；
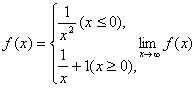（2）
；
（3）
；
（4）
.
解：（1）显然，当
时，
；当
时，
.即
，故
不存在.
（2）显然，
，故
不存在.
（3）∵
，∴
.
（4）当时，
，当时，
，所以不存在.
例2．求下列各式的极限：
（1）
；
点评：当
在
处连续时，则可用直接代入法，即
=
.
（2）
；
（3）
；
（4）
；
（5）
；
（6）
.
例3．已知
，求
、
的值.
解：∵
∴
为方程
的根，
，
又
，∴
.
三、同步练习：《高考三人行—学生用书》P340