数列极限复习指导

数列极限复习指导

一、重点难点分析：
　　1.三个最基本的极限
　　(1)常数数列的极限就是其本身，即：C=C。 (2)=0。 (3)当q<1时，qⁿ=0。
　　这三个最基本的极限是求复杂数列极限的基础和化归方向。
　2.数列极限四则运算法则：
　　如果a_n=A, b_n=B, 那么： 　　(a_n±b_n)=a_n±b_n=A±B。
　　(a_n·b_n)=a_n·b_n=A·B。　== (b_n≠0，B≠0)。
　　== (a_n≥0, A≥0)。
　　应特别注意理解：
　　(1)公式成立的条件：公式成立的前提是{a_n}与{b_n}都存在极限。
　(2)公式的实质：是四则运算与取极限这两种运算可以变换顺序。
　　(3)公式的推广：公式中的两项的和，差，积可以推广到有限个项，但是它们都不能推广到无限个。
　　3.无穷数列各项的和
　　(1)无穷递缩等比数列：
　　当公比q<1时无穷等比数列{a_n}称为无穷递缩等比数列。 S_n==。
　　则称这个极限叫做无穷递缩等比数列各项的和，用S表示，即S=。
　　(3)其它无穷数列各项的和：
　　若无穷数列{b_n}不是等比数列，但可求得前n项和 T_n，且T_n=t。
　　则无穷数列{b_n}的各项和存在，且为：S=T_n=t。
　　4.求数列极限的方法与基本类型：
　　1)．求数列极限的基本思路是“求和——变形——利用极限的运算法则求解”，而在求解前应先化为三个重要的极限。
　　2)．常见的几类数列极限的类型和方法有： 　①型：分子分母分别求和再化简转化
　　②型：分子分母分别求和再化简转化 　③已知极限值定参数：待定系数法
　　3)．要注意极限运算法则的使用范围，以及特殊极限的使用条件。
　　4)．实际运用中极限思想应引起注意。
　　二、应用举例：
　　例1．求下列极限：
　　(1) 　　(2)
　　(3)
　　解：(1) ∵   　　∴ 原式=。
　　(2)∵
　　　　=　　∴ 原式=。
　　(3)∵
　　　　
　　∴ 原式。
　　例2．设数列a₁,a₂,……a_n……的前n项和S_n与a_n的关系是：，其中b是与n无关的常数且b≠-1。　①求a_n和a_n-1的关系式。　②写出用n和b表示a_n的表达式。
　　③写0<b<1时，求极限。
　　解析：(1)∵
　　　　　　　 　　
　　∴
　　(2)∵ , ∴ 。
　　∴
　　 　　
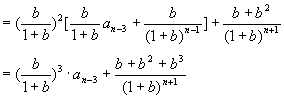
　　由此猜想。　 证明（略）
　　把代入上式得：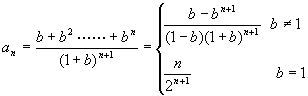
　　(3)
　　　　　
　　∵ 0<b<1时，， 　　∴ 。
　　例3．(1) 已知，求a,b的值。
　　(2) 已知数列{a_n}的前n项和S_n=1+ka_n (k为不等于1的常数) 且，求k的取值范围。
　　解析：(1)由条件知该数列极限存在且为0，所以原式可变形为：。
　　显然，当且仅当a=1时，左边才有极限，而要使其极限为0，则-(a+b)=0，解得b=-1，因此a=1, b=-1。
　　(2) S_n=1+ka_n, 当n=1时，a₁=S₁=1+ka₁, ∴ ，当n≥2时，a_n=S_n-S_n-1=ka_n-ka_n-1,
(k-1)a_n=ka_n-1，∴ (常数) 　∴ ，由得,
∴ ，故 ，∴k²<k²-2k+1，∴。
　例4．（2001全国高考）已知等差数列前三项为a,4,3a，前n项和为S_n, S_k=2550。
　　(1) 求a及k的值；(2) 求。
　　解析：(1) 设该数列为{a_n}, 则a₁=a, a₂=4, a₃=3a, S_k=2550。
　　由已知a+3a=2×4，∴a₁=a=2，公差d=a₂-a₁=4-2=2。
　　由得k²+k-2550=0，解得k=50，或k=-51。 　∴a=2, k=50。
　　(2)由得 S_n=n(n+1)
　　∴ 。
　　∴ 。
　

　训练题：
　　1．求下列极限
　　(1) 　　(2)
　　(3)　　(4)
　　2．设首项为1，公比为q的等比数列的前n项和为S_n，求。
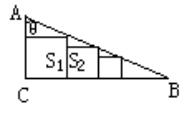　　3．RtΔABC中，AC=a, ∠A=θ, ∠C=90°，排列着无限多个正方形。（如图所示），其中面积依次为S₁，S₂，S₃，……。试将这些正方形的面积之和S用a和θ表示，若S为RtΔABC的面积的，试确定θ的值。

　　参考答案：　
　　1. (1) 　　(2) 2　　(3) 当a>b时，原式=，当a<b时，原式=。　　(4)
　　2. ∵ ， ∴ 。
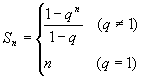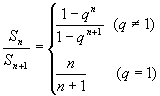　　①当q=1时，。 　②当q≠1时， 若0<q<1，，
　　若q>1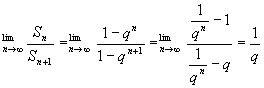，。 故：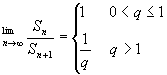
　　3．设第n个正方形的边长为x_n,考虑图中三角形的长关系是
　　 　，∴ ，又，
　　∴ ，∴ {S_n}是首项，公比为的等比数列。
　　又，∴ S=，而，
　　∴ ，∴ ，∴ 。