数形结合思想方法

八、数形结合思想方法

中学数学的基本知识分三类：一类是纯粹数的知识，如实数、代数式、方程（组）、不等式（组）、函数等；一类是关于纯粹形的知识，如平面几何、立体几何等；一类是关于数形结合的知识，主要体现是解析几何。数形结合一是一个数学思想方法，应用主要是借助形的直观性来阐明数之间的联系，其次是借助于数的精确性来阐明形的某些属性。

数形结合的思想，其实质是将抽象的数学语言与直观的图像结合起来，关键是代数问题与图形之间的相互转化。

Ⅰ、再现性题组：

1.　设命题甲：0<x<5；命题乙：x－2<3，那么甲是乙的_____。 （90年全国文）

A.充分非必要条件　 B.必要非充分条件　 C.充要条件　 D.既不充分也不必要条件

2.　若log2<log2<0，则_____。(92年全国理)

A. 0<a<b<1　　 B. 0<b<a<1　　 C. a>b>1　　 D. b>a>1

3.　如果x≤,那么函数f(x)＝cosx＋sinx的最小值是_____。 (89年全国文)

A.　　　　　 B. －　　　　 C. －1　　　　　  D.

4.　如果奇函数f(x)在区间[3,7]上是增函数且最小值是5，那么f(x)的[-7,-3]上是____。(91年全国)

A.增函数且最小值为－5　　　　　　　  B.增函数且最大值为－5

C.减函数且最小值为－5　　　 　　　　 D.减函数且最大值为－5　

5.　设全集I＝{(x,y)x,y∈R}，集合M＝{(x,y) ＝1}，N＝{(x,y)y≠x＋1}，那么等于_____。　(90年全国)

A.　φ　　　　  B. {(2,3)}　　　C. (2,3)　　　D. {(x,y)y＝x＋1　

6.　如果θ是第二象限的角，且满足cos－sin＝,那么是_____。

A.第一象限角　　B.第三象限角　　C.可能第一象限角，也可能第三象限角　　D.第二象限角

7.　已知集合E＝{θcosθ<sinθ，0≤θ≤2π}，F＝{θtgθ<sinθ}，那么E∩F的区间是_____。

A. (,π)　　B. (,)　 C. (π, )　 D. (,)　　　 （93年全国文理）

8.　若复数z的辐角为，实部为－2，则z＝_____。

A. －2－2ｉ　 B. －2＋2ｉ　　C. －2＋2ｉ　　D. －2－2ｉ

9.　如果实数x、y满足等式(x－2)＋y＝3，那么的最大值是_____。　(90年全国理)

A. 　　　 B. 　　　C.　　　　　D.

10.　　　 满足方程z＋3－ｉ＝的辐角主值最小的复数z是_____。

【注】 以上各题是历年的高考客观题，都可以借助几何直观性来处理与数有关的问题，即借助数轴（①题）、图像（②、③、④、⑤题）、单位圆（⑥、⑦题）、复平面（⑧、⑩题）、方程曲线（⑨题）。

y 　4　　　 　y=1-m 　1 　O　　2　 3　　x

Ⅱ、示范性题组：

例1. 若方程lg(－x＋3x－m)＝lg(3－x)在x∈(0,3)内有唯一解，求实数m的取值范围。

【解】 原方程变形为 　　即：

设曲线y＝(x－2) , x∈(0,3)和直线y＝1－m，图像如图所示。由图可知：① 当1－m＝0时，有唯一解，m＝1;　　　②当1≤1－m<4时，有唯一解，即－3<m≤0,

∴　m＝1或－3<m≤0

【注】 方程解、不等式解集、函数性质等的讨论，借助于图像直观解决，简单明了。此题也可用代数方法来讨论方程的解的情况，还可用分离参数法来求（也注意结合图像分析只一个x值）。

y　　A 　　　　　  D 　　　 O　　B　　 x 　　　　　  C

例2. 设z＝5，z＝2, z－＝，求的值。

【分析】 利用复数模、四则运算的几何意义，将复数问题用几何图形帮助求解。

【解】 如图，设z＝、z＝后，则＝、＝如图所示。

由图可知，＝，∠AOD＝∠BOC，由余弦定理得：cos∠AOD＝＝

∴ ＝(±ｉ)＝2±ｉ

【注】 复数问题可利用几何意义而几何化。也可设复数的代数形式、三角形式转化成代数问题或三角问题，还可直接利用复数性质求解。

例3. 直线L的方程为：x＝－　(p>0),椭圆中心D(2＋,0)，焦点在x轴上，长半轴为2，短半轴为1，它的左顶点为A。问p在什么范围内取值，椭圆上有四个不同的点，它们中每一个点到点A的距离等于该点到直线L的距离？

【分析】 由抛物线定义，可将问题转化成：p为何值时，以A为焦点、L为准线的抛物线与椭圆有四个交点，再联立方程组转化成代数问题（研究方程组解的情况）。

【解】 由已知得：a＝2，b＝1, A(,0)，设椭圆与双曲线

……

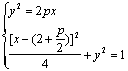【注】 判别式法（注意解的范围）、定义法、数形结合法、转化思想、方程思想等知识综合运用。

例4. 设a、b是两个实数，A＝{(x,y)x＝n，y＝na＋b} （n∈Z），B＝{(x,y)x＝m，y＝3m＋15}　(m∈Z)，C＝{(x,y)x＋y≤144}，讨论是否存在a、b，使得A∩B≠φ与(a,b)∈C同时成立。(85年高考)

【解】 由A∩B≠φ得：na＋b＝3n＋15 ;

设动点(a,b)在直线L：nx＋y＝3n＋15上，且直线与圆x＋y＝144有公共点，

所以圆心到直线距离d＝＝3(＋)≥12

∵ n为整数　 ∴ 上式不能取等号，故a、b不存在。

【注】 集合转化为点集（即曲线），而用几何方法研究。此题也属探索性问题用数形结合法解。

Ⅲ、巩固性题组：

1.　　已知5x＋12y＝60，则的最小值是_____。

A. 　　 B. 　　 C. 　　 D. 1

2.　　已知集合P＝{(x,y)y＝}、Q＝{(x,y)y＝x＋b}，若P∩Q≠φ，则b的取值范围是____。

A. b<3　　 B.　b≤3　　 C. －3≤b≤3　　 D.　－3<b<3

3.　　方程2＝x＋2x＋1的实数解的个数是_____。

A.　1　　　B.　2　　 C.　3　　 D.以上都不对

4.　　方程x＝10sinx的实根的个数是_______。

5.　　若不等式m>x－1＋x＋1的解集是非空数集，那么实数m的取值范围是_________。

6.　　设z＝cosα＋ｉ且z≤1,那么argz的取值范围是____________。

7.　　若方程x－3ax＋2a＝0的一个根小于1，而另一根大于1，则实数a的取值范围是______。

8.　　sin20°＋cos80°＋sin20°·cos80°＝____________。

9.　　解不等式：　 >b－x

10. 设A＝{x<1x<3}，又设B是关于x的不等式组的解集，试确定a、b的取值范围，使得AB。　（90年高考副题）

11. 定义域内不等式〉x＋a恒成立，求实数a的取值范围。

12. 已知函数y＝＋，求函数的最小值及此时x的值。

13. 已知z∈C，且z＝1，求(z＋1)(z－ｉ)的最大值。

14. 若方程lg(kx)＝2lg(x＋1)只有一个实数解，求常数k的取值范围。