数学奥林匹克高中训练题（15）
第一试
一、选择题（本题满分36分，每小题6分）
2．(训练题20)把直线
沿
轴平移
个单位，再沿
轴平移
个单位，所得到的直线与原直线重合，则原直线的斜率为(B)．
(A) 不存在 (B) 
(C) 
(D) 
3．(训练题20)三棱锥
中，
平面
．则
与
的关系为(D)．
(A) 
(B) 
(C) (D) 不确定
4．(训练题20)设递增正数列
是分母为60的既约真分数．则
(A)．
(A) 0 (B)8 (C) 16 (D) 30
5．(训练题20)从正方体的８个顶点中取出３个顶点使至少有两个顶点在同一棱上，其取法数为(B)．
(A)44 (B)48 (C)50 (D) 52
6．(训练题20)存在
满足
，且使
成立的充要条件是(B)．
(A) 
(B) 
(C) 
(D) 
二、填空题（本题满分54分，每小题9分）
1．(训练题20)已知
则
．
2．(训练题20)递推数列，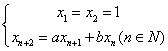
， 若
是使
的最小自然数，则
= 0 ．
3．(训练题20)在平面
上有一个
，
．在平面的两侧分别有一点
，满足
．则
8 ．
5．(训练题20)在双曲线
上任取三点
，则垂心
的轨迹方程为．
6．(训练题20)对复数，解析式
的最小值为 
．
第二试
一、(训练题20)(本题满分25分)在的
边上任取一点
作
交
于
，连
．求证:
的面积不超过原三角形面积的
．
二、(训练题20)(本题满分25分)求证:对于任给的正数
，必存在一个自然数
，使每一个大于的自然数
都有唯一的自然数
，使
．
三、(训练题20)(本题满分35分)对于坐标平面上的整点集
，求证:从中任取11个点时必存在3个点，两两之间连线的斜率存在且不为零．
四、(训练题20)(本题满分35分)设
.取
(无顺序),若
或
时，则称
为”包含子集对”，否则称为非包含子集对，问
中包含子集对多还是非包含子集多?证明你的结论.