全国高考数学模拟试卷（二）
一．选择题（本大题共有12道小题，每小题5分，计60分）
1．设P、Q是两个非空集合，定义P*Q=
，若P=
Q=
，则P*Q中元素的个数是…………………………………………………（ ）
A．4个 B．7个 C．12个 D．16个
2．过抛物线y2=4x的焦点F作垂直于x轴的直线，交抛物线于A、B两点，则以F为圆心，AB为直径的圆方程是……………………………………………………………………（ ）
A．(x－1)2+y2=1 B．(x－1)2+y2=2
C．(x－
)2+y2=4
D．(x－1)2+y2=4
3．已知m，
是异面直线，给出下列四个命题：①必存在平面
，过m且与都平行；②必存在平面 
，过m且与垂直；③必存在平面r，与m，都垂直；④必存在平面w, 与m，的距离都相等。
其中正确的结论是………………………………………………………………………（ ）
A．①② B．①③ C．②③ D．①④
4．要得到函数y=sin2x的图象，可以把函数y=sin(2x－
)的图象…………………( )
A．向左平移
个单位
B．向右平移个单位
C．向左平移
个单位
D．向右平移 个单位
5.已知真命题：“a≥b
c>d”和“a<b
”,那么“c≤d”是“e≤f”的……（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又必要条件
6．（理）从8盒不同的鲜花中选出4盆摆成一排，其中甲、乙两盆不同时展出的摆法种数为…………………………………………………………………………………………（ ）
A．1320 B．960 C．600 D．360
（文）从8盆不同的鲜花中选出4盆摆成一排，其中甲、乙两盆有且仅有一盆展出的不同摆法种数为…………………………………………………………………………………（ ）
A．1320 B．960 C．600 D．360
7．设函数f(x)是定义在R上的以3为周期的奇函数，若f(x)>1，f(2)= 
，则
……………………………………………………………………………………………（ ）
A.a<
B.a<
C.a>
D.－1<a<
8．已知log
, 0<a<1，则x1,x2,x3的大小关系是………（ ）
A．x3<x2< x1 B．x2<x1< x3 C．x1<x3< x2 D．x2<x3< x1
9．（文）已知直线y=kx+1与曲线y=x3+ax+b切于点(1，3)，则b的值为………（ ）
A．3 B．－3 C．5 D．－5
（理）设曲线y=
和曲线y=
在它们交点处的两切线的夹角为
，则tan的值为…………………………………………………………………………………………（ ）
A．1
B．
C．
D．
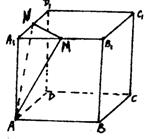
10．如图，在棱长为3的正方体ABCD－A1B1C1D1中，M、N分别是棱A1B1、A1D1的中点，则点B到平面AMN的距离为……………………（ ）
A．
B.
C. 
D.2
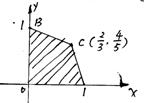11．如图，目标函数u =ax－y的可行域为四边形的OACB（含边界），若(
)是该目标函数的最优解，则a的取值范围是……………………………………………（ ）
A.
B.
C.
D.
12．已知
为锐角，sin
,cos=y, cos(
)=－
,则y与x的函数关系式为……………………………………………………………………………………………（ ）
A.y=－
B.y=－
C.y=－
D.
y=－
二．填空题（本大题共有4小题，每小题4分，计16分）
13．设f(x)= x5－5x4+10x3－10x2+5x+1，则f(x)的反函数为 f－1(x)=________。
14.某校有高中生1200人，初中生900人，老师120人，现用分层抽样的方法从所有师生中抽取一个容量为N的样本；已知从初中生中抽取人数为60人，那么N=__________。
15．在平面几何中有：Rt△ABC的直角边分别为a,b，斜边上的高为h，则
。类比这一结论，在三棱锥P—ABC中，PA、PB、PC两点互相垂直，且PA=a，PB=b，PC=c，此三棱锥P—ABC的高为h，则结论为_______-。
16．某大楼共有20层，有19人在第一层上了电梯，他们分别要去第2层至第20层，每层1人，而电梯只允许停 1次，可只使1人满意，其余18人都要步行上楼或下楼，假设乘客有向下走1层的不满意度为1，每向上走一层的不满意度为2，所有人的不满意度之和为S，为使S最小，电梯应当停在第___________层；
三．解答题（本大题共有6道题目，计74分）
17．（本题满分12分）已知锐角△ABC中，三个内角为A、B、C，两向量
，
是共线向量。
（I）求∠A的大小；
（II）求函数y=2sin2B+cos(
)取最大值时，∠B的大小。
18．（本题满分12分）为了测试甲、乙两名射击运动员的射击水平，让他们各向目标靶射击10次，其中甲击中目标7次，乙击中目标6次。若再让甲、乙两人各自向目标靶射击3次，求：
（I）甲运动员恰好击中目标2次的概率是多少？
（II）（文）两名运动员都恰好击中目标2次的概率是多少？（结果保留两位有效数字）
（理）分别求甲、乙两名运动员击中目标次数
、
的数学期望E
、E
的值。
19．（本题满分12分）在正四棱柱ABCD－A1B1C1D1中，侧棱长是底面边长的2倍，P是侧棱CC1上的任意一动点。
（I）求证：不论P在侧棱CC1上何位置，总有BD⊥AP；
（II）若CC1=3C1P，求平面AB1P与平面ABCD所成的二面角的余弦值；
（III）当点P在侧棱CC1何处时，AP在平面B1AC上的射影是∠B1AC的平分线。
20．（本题满分12分）设f(x)=x3+3x2+px, g(x)=x3+qx2+r，且y=f(x)与y=g(x)的图象关于点（0，1） 对称。
（I）求p、q、r的值；
（II）若函数g(x)在区间(0，m)上递减，求m的取值范围；
（III）若函数g(x)在区间
上的最大值为2，求n的取值范围。
21．（本题满分12分）已知数列 
的前项为a1=2, 前n项和为Sn ,且对任意的n∈N+，n≥2，an总是3Sn－4与2－
Sn－1的等差中项。
（1）求通项an;
(II)证明：
（III）（理）含b
Tn、Rn分别为
的前n项和是否存在正整数n，使得Tn<Rn，若存在，请求出所有n的值，否则请说明理由。
(文) 设f(n)=an,g(n)=Sn, 解不等式：f2(n)>10－g(n)
22.(本题满分14分)已知动点P与双曲线x2－y2=1的两个焦点F1、F2的距离之和为定值，且cosF1PF2的最小值为－。
（I）求动点P的轨迹方程;
（II）设M（0,－1），若斜率为k(k≠0)的直线与P的轨迹交于不同的两点A、B，试求k的取值范围，使MA=MB；
（文）若直线:y=x+m与P的轨迹交于不同的两点A、B，且
，M（0，－1），求M到直线的距离。
高考数学模拟试卷（二）参考答案
一．1．C C
2．D F(1,0 ) A(1, 2) B(1,－2) r=2 ∴方程为(x－1)2+y2=4
3.D(1)平移m,使m与相交,设两相交直线确定的平面为,作∥且m
.正确.
(2)仅当⊥m时成立.不正确. (3)与同一平面垂直的直线平行.不正确.
(4)过m, 公垂线中点的与m, 都平行的平面w,正确.
4.A y=sin(2x－)=sin2(x－)
5.A
设命题a
b为p. c>d为q. 则a<b为
∵p是q的充分条件 ∴
的充分条件．∴c
的充分不必要条件．
6.(理)A 设甲、乙同时摆出的事件为A; 
的事件数为A
=1320
（文）B C
7．D f(1)=f(－2)>1 ; f(2)=－f(－2)<－1; 
∴－1<a<
8.D ∵0<a<1 ∴a<1<a+1<
∴x2<1<x3<x1
9.(文)A直线y=kx+1 ; y′=k; 曲线y=x3+ax+b; y′=3x2+a
∴
∴
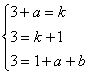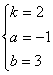
（理）Ｃ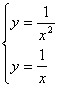 
∴x=1，∴交点（１，１）
两切线分别为
; tan
10.D 体积法．ＶＮ－ＭＡＢ＝ＶＢ－ＭＮＡ
设所求距离为d．Ｓ△ＭＮＡ＝
，Ｓ△ＡＢＭ＝－; d·Ｓ△ＭＮＡ
Ｓ△ＡＢＭ·A1N ; d=2
11.B a
∴a
12.A cos
; sin
y=cos
∵1>y>0; ∴0<－
; ∴x>
二、13. 
1;
f(x)=－[C
]+2
=－(1－x)5+2 =(x－1)5+2; ∴f－1(x)=
14. 14g; N=
15.
16. 14 设停在n层，则（20－n）人上楼，（n－2）人下楼，
S=2·
=
，n=14时S最小
三17.解：(1)
=(2－2sinA,cosA+sinA)，
=(sinA－cosA,1+sinA)，∵//
∴（2－2sinA）(1+sinA)－(cosA+sinA)(sinA－cosA)=0; ∵△ABC为锐角形，sinA=
∴A=60° （2）y=2sin2B+cos()=2sin2B+cos(
)=2sin2B+cos(2B－60°)
=1－cos2B+cos(2B－60°) =1+sin(2B－30°) 当B=60°时取最大值2
18．解（I）设甲击中目标2次的事件为A，P（A）=C
×(0.7)2×(1－0.7)=0.441，
(II)(文) 设乙击中目标2次的事件为B，P（B）=C
×(0.6)2×(1－0.6)=0.432，P(A·B)=P(A)·P(B)=0.190512
; (理)甲射中一次概率 C
×(1－0.7)2=0.189，射中二次概率C
2×(1－0.7)2=0.441，射中三次概率C
(0.7)3=0.343，E=1×0.189+2×0.441+3×0.343=2.1。乙射中一次概率C
×(1－0.6)2=0.288，
射中二次概率C
×(1－0.6)=0.432，射中三次概率C
=0.216，E=1×0.288+2×0.437+0.216×3=1.8。
19．（I）证明：∵正四棱柱ABCD-A1B1C1D1; ∴PC⊥面ABCD，∴P在ABCD上射影为C
又∵BD⊥AC ∴AP⊥BD
（II）解：延长BC，B1P，交于点R，过B作BQ⊥AR于Q，连结B1Q
∴B1在面ABCD上射影为C ; BQ⊥AR，AR
面ABCD; ∴B1Q⊥AR
∴∠B1QB为二面角B1—AR—B的平面角。设P底边长为G，则BQ=
tan∠B1QB=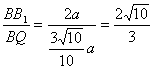
, cos∠B1QB=
;
(III)即∠B1AP=∠PAC, 设CP=b, cos∠PAC=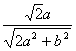
cos∠B1AP=
, ∴b=
20.(I)设M
f(x), M(x,x3+3x2+px), M关于点（0,1）对称的点M′（－x,2－(x3+3x2+px)）g(x)
∴－x3+qx2+r=2－(x3+3x2+px), ∴q=－3,p=0,r=2
(II)g(x)=x3－3x2+2, g′(x)=3x2－6x, 令g′(x)<0, 则x(0,2)
∴0<m≤2
（III）g(x)在
上增
在[0,2]上减 在
上增
令g(x)=2 x=0或3 ∴n
21.(I)n
时，2an=3Sn－4+2－
即2（Sn－Sn－1）=3Sn－4+2－.
Sn=
, Sn－4=
, Sn－4=()n－1·(a1－4)=－2()n－1，Sn=4－2()n－1，
Sn－1=4－2()n－2。 ∴An=Sn－Sn－1=()n－2，n=1时也成立 ∴an=()n－2
(II)Sn=4－()n－2， 要证
，只要证 Sn·Sn+2<S
，
左边=[4－()n－2][4－()n]=[16－4[()n－2+()n]+()2n－2。
右边=
左边－右边=8()n－1－4[()n－2+()n]=()n－4－()n－4－()n－2=－()n－2<0
∴左边<右边 ∴（log2Sn+log2Sn+2）<log2Sn+1.
(III)(理) bn=2n－1 Cn=log2(2n)2=2n Tn=2n+1－n－2 Rn=n2+n
若Tn<Rn 即2n+1<n2+2n+2,
当n=1，2时，Tn<Rn, 验证n=4,5时，Tn>Rn 当n4,5时，Tn>Rn,
n≥6时用二项式定理进行证明2n+1=(1+1)n+1=C
=2(n+2)+n2+n>n2+2n+2.
∴当n≥3时，Tn>Rn ∴只有n=1，2时Tn<Rn ∴不存在
（文）f(n)=an=()n－2 g(n)=Sn=4－()n－2
f2(n)－110－g(n)=[()n－2]2－10+4－()n－2=()2n－4－()n－2－6
令()n－2=t ,(t>0) f2(n)－[10－g(n)]=t2－t－6>0
∴t>3 ∴()n－2>3 ∴n<2+
∵nN+
∴n=1,2
22.(I)设P的轨迹方程为
（a>2）
cosF1PF2最小值为
，a2=3
∴P点轨迹方程为
（II）（理）设A（x,y）,B(x2,y2)
∵
∴MA2=MB2
∴x
+(y1+1)2=x22+(y2+1)2 ∴(x1+x2)(x1－x2)+(y1+y2+2)(y1－y2)=0 ∴
∴(x1+x2)+k(y1+y2+2)=0
(A)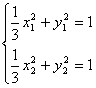 
两式相减得
∴
代入（A） k(－2y1－2y2+2)=0 ∵k≠0
∴y1+y2=1 ∴x1+x1=－3k 设直线方程为:y=kx+b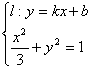 
(3k2+1)x2+6bkx+3b2－3=0 x1+x2=
2b=3k2+1 △=(6bk)2－4(3k2+1)(3b2－3)>0 ∴3k2+1>b2 ∴3k2+1>(
)2
k2<1 ∴k∈（－1，1） （文）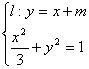
4x2+6mx+3m2－3=0 设A（x1,y1）,B(x2,y2) ∴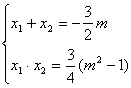
x1－x2=
AB=
∴m=±
m=时，
M到距离d1=
m=－时，
M到距离d2=－