全国高考数学试题2
(理工农医类)
一.选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)圆![]() 的圆心到直线
的圆心到直线![]() 的距离是
的距离是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(2)复数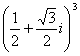 的值是
的值是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3)不等式![]() 的解集是
的解集是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(4)在![]() 内,使
内,使![]() 成立的
成立的![]() 取值范围为
取值范围为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(5)设集合![]() ,
,![]() ,则
,则
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6)点![]() 到曲线
到曲线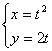 (其中参数
(其中参数![]() )上的点的最短距离为
)上的点的最短距离为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(7)一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么这个圆锥截面顶角的余弦值是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(8)正六棱柱![]() 的底面边长为
的底面边长为![]() ,侧棱长为
,侧棱长为![]() ,则这个棱柱的侧面对角线
,则这个棱柱的侧面对角线![]() 与
与![]() 所成的角是
所成的角是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(9)函数![]() 是单调函数的充要条件是
是单调函数的充要条件是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10)函数![]() 的图象是
的图象是
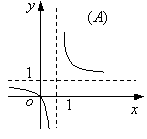
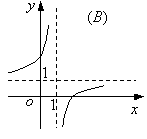
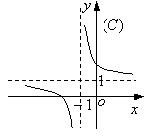
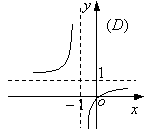
(11)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
(A)8种(B)12种(C)16种(D)20种
(12)据2002年3月5日九届人大五次会议《政府工作报告》:“2001年国内生产总值达到95 933亿元,比上年增长7.3%.”如果“十·五”期间(2001年—2005年)每年的国内生产总值都按此年增长率增长,那么到“十·五”末我国国内年生产总值约为
(A)115 000亿元(B)120 000亿元(C)127 000亿元(D)135 000亿元
二.填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
(13)函数![]() 在
在![]() 上的最大值与最小值的和为3,则
上的最大值与最小值的和为3,则![]() 。
。
(14)椭圆![]() 的一个焦点是
的一个焦点是![]() ,那么
,那么![]() 。
。
(15)![]() 的展开式中
的展开式中![]() 项的系数是 。
项的系数是 。
(16)已知函数![]() ,那么
,那么
![]() 。
。
三.解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)
已知![]() ,
,![]() 。求
。求![]() 、
、![]() 的值。
的值。
(18)(本小题满分12分)
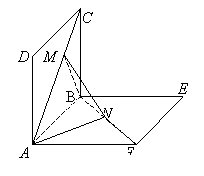
如图,正方形![]() 、
、![]() 的边长都是1,而且平面
的边长都是1,而且平面![]() 、
、![]() 互相垂直。点
互相垂直。点![]()
在![]() 上移动,点
上移动,点![]() 在
在![]() 上移动,若
上移动,若![]()
![]() 。
。
(Ⅰ)求![]() 的长;
的长;
(Ⅱ)当![]() 为何值时,
为何值时,![]() 的长最小;
的长最小;
(Ⅲ)当![]() 长最小时,求面
长最小时,求面![]() 与面
与面![]() 所成的二面角
所成的二面角![]() 的大小。
的大小。
(19)(本小题满分12分)
设点![]() 到点
到点![]() 、
、![]() 距离之差为
距离之差为![]() ,到
,到![]() 轴、
轴、![]() 轴距离之比为
轴距离之比为![]() 。
。
求![]() 的取值范围。
的取值范围。
(20)(本小题满分12分)
某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的![]() ,并且每年新增汽车数量相同。为保护城市环境,要求该城市汽车保有量不超过
,并且每年新增汽车数量相同。为保护城市环境,要求该城市汽车保有量不超过![]() 万量,那么每年新增汽车数量不应超过多少辆?
万量,那么每年新增汽车数量不应超过多少辆?
(21)(本小题满分12分)
设![]() 为实数,函数
为实数,函数![]() ,
,![]() 。
。
(Ⅰ)讨论![]() 的奇偶性;
的奇偶性;
(Ⅱ)求![]() 的最小值。
的最小值。
(22)(本小题满分14分)
设数列![]() 满足
满足![]() ,
,![]()
(Ⅰ)当![]() 时,求
时,求![]() ,
,![]() ,
,![]() ,并由此猜想出
,并由此猜想出![]() 的一个通项公式;
的一个通项公式;
(Ⅱ)当![]() 时,证明对所有的
时,证明对所有的![]() ,有
,有
(ⅰ)![]() ;
;
(ⅱ)![]() 。
。