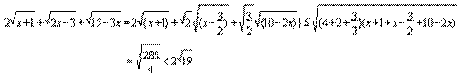全国高中数学联赛第一试
一、选择题(每小题6分,满分36分)
1.
删去正整数数列1,2,3,……中的所有完全平方数,得到一个新数列.这个新数列的第2003项是
(A)2046 (B)2047 (C)2048 (D)2049
2. 设a, bÎR, ab≠0,那么,直线
ax-y+b=0和曲线 bx2+ay2=ab 的图形是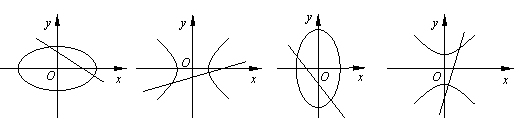

(A)
(B)
(C) (D)
3.
过抛物线y2=8(x+2)的焦点F作倾斜角为60°的直线.若此直线与抛物线交于A,B两点,弦AB的中垂线与x轴交于P点,则线段PF的长等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)8
(D)8![]()
4.
若xÎ[-![]() ,-
,-![]() ],则y= tan(x+
],则y= tan(x+![]() )-tan(x+
)-tan(x+![]() )+cos(x+
)+cos(x+![]() )的最大值是
)的最大值是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.
已知x,y都在区间(-2,2)内,且xy=-1,则函数u=![]() +
+![]() 的最小值是
的最小值是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.
在四面体ABCD中,设AB=1,CD=![]() ,直线AB与CD的距离为2,夹角为
,直线AB与CD的距离为2,夹角为![]() ,则四面体ABCD的体积等于
,则四面体ABCD的体积等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题(每小题9分,满分54分)
7. 不等式x3-2x2-4x+3<0的解集是__________.
8.
设F1,F2是椭圆![]() 的两个焦点,P是椭圆上的点,且PF1:PF2=2:1,则△PF1F2的面积等于__________.
的两个焦点,P是椭圆上的点,且PF1:PF2=2:1,则△PF1F2的面积等于__________.
9.
已知A={xx2-4x+3<0,xÎR}, B={x![]() ≤0, x2-2(a+7)x+5≤0,xÎR}.若AÍB, 则实数a的取值范围是____________.
≤0, x2-2(a+7)x+5≤0,xÎR}.若AÍB, 则实数a的取值范围是____________.
10.
已知a,b,c,d均为正整数,且logab=![]() , logcd=
, logcd=![]() ,若a-c=9, 则b-d=________.
,若a-c=9, 则b-d=________.
11. 将八个半径都为1的球分两层放置在一个圆柱内,并使得每个球和其相邻的四个球相切,且与圆柱的一个底面及侧面都相切,则此圆柱的高等于________.
12.
设Mn={(十进制)n位纯小数0.![]() ai只取0或1(i=1,2,…,n-1),an=1},Tn是Mn中元素的个数,Sn是Mn中所有元素的和,则
ai只取0或1(i=1,2,…,n-1),an=1},Tn是Mn中元素的个数,Sn是Mn中所有元素的和,则![]() =_______.
=_______.
三、解答题(每小题20分,满分60分)
1.
已知![]() ,证
,证![]()
2.
设A、B、C分别是复数![]() ,
,![]() ,
,![]() 对应的不共线三点。
对应的不共线三点。
证:曲线![]() 与
与![]() 中平行于AC的中位线只有一个公共点,并求出此点。
中平行于AC的中位线只有一个公共点,并求出此点。
3.
一张纸上画有半径为R的圆O和圆内一定点A,且OA=a,折叠纸片,使圆周上某一点![]() 刚好与A点重合,这样的每一种折法,都留下一条直线折痕,当
刚好与A点重合,这样的每一种折法,都留下一条直线折痕,当![]() 取遍圆周上所有点时,求所有折痕所在直线上点的集合。
取遍圆周上所有点时,求所有折痕所在直线上点的集合。
第二试
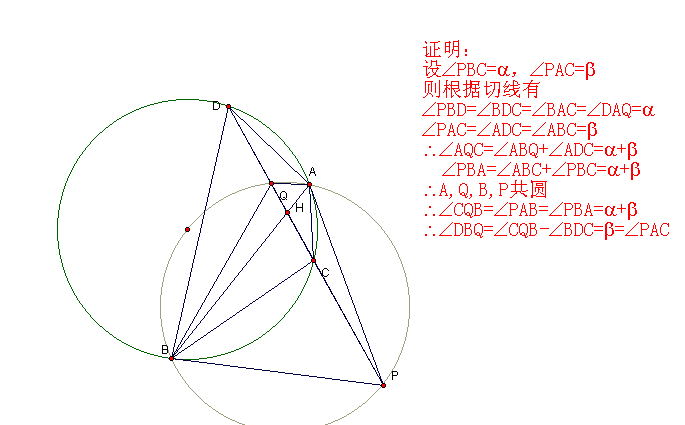
1、过圆外一点P作圆的两条切线和一条割线,切点为A、B,所作割线交圆于C、D两点,C在P、D之间,在弦CD上取一点Q,使![]() 。求证:
。求证:![]()
2、设三角形的三边长分别是整数![]() 且
且![]() ,已知
,已知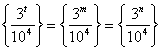 ,其中
,其中![]() ,求这种三角形周长的最小值。
,求这种三角形周长的最小值。
3、由n个点和这些点之间的![]() 条连线段组成一个空间图形,其中
条连线段组成一个空间图形,其中![]() ,
,![]() ,已知此图中任四点不共面,每点至少有一条连线段,存在一点至少有q+2条连线段。证明:图中必存在一个空间四边形(即由A,B,C,D和AB、BC、CD、DA组成的图形)。
,已知此图中任四点不共面,每点至少有一条连线段,存在一点至少有q+2条连线段。证明:图中必存在一个空间四边形(即由A,B,C,D和AB、BC、CD、DA组成的图形)。
全国高中数学联赛(答案)
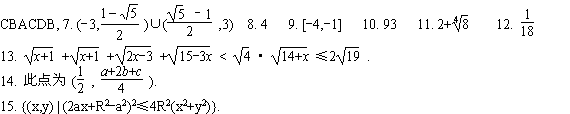 13题解答:
13题解答:
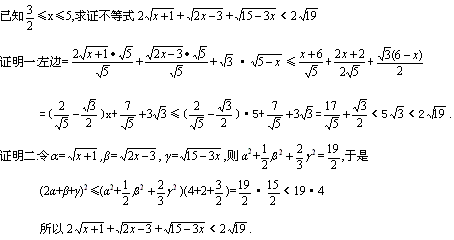
证明三:
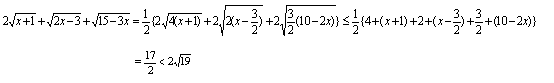
证明四: