全国高中数学联赛模拟试题(四)

全国高中数学联赛模拟试题(四)

第一试

一、选择题(共36分)

1.　　 设变量x满足x²＋bx≤－x(b＜－1)，且f(x)＝x²＋bx的最小值为－，则b＝(　　　)
A.－　　　　　　B.－　　　　　　　 C.－2　　　　　　　 D.－或－

2.　　 已知x∈()，给出下列六个不等式
①sin(sinx)＜cos(cosx)　　　　　　　　 ②sin(cosx)＜sin(sinx)
③cos(sinx)＜cos(cosx)　　　　　　　　 ④cos(sinx)＜sin(sinx)
⑤cos(cosx)＜sin(cosx)　　　　　　　　 ⑥sin(cosx)＜cos(sinx)
其中成立的个数为　　　　　　　　　　　　　　　　　　　　　　　　　 (　　　)
A.3　　　　　　　　B.4　　　　　　　　 C.5　　　　　　　　 D.6

3.　　 设x₁，x₂是实系数一元二次方程ax²＋bx＋c＝0的根，若x₁是虚数，是实数，则
S＝1＋的值为　　　　　　　　　  (　　　)
A.0　　　　　　　　B.－998　　　　　　 C.998　　　　　　　 D.－997

4.　　 在空间，从一点O出发引四条射线OA，OB，OC，OD，如果∠AOB＝∠BOC＝∠DOA＝∠AOC＝θ，则θ的值为　　　　　　　　　　　　　　　　　　　　　　　  (　　　)
A.π－arcsin　　　B.π－arcsin　　　 C.π－arccos　　　 D.π－arccos

5.　　 已知a＞，则y＝(sinx＋a)(cosx＋a)的最小值为　　　　　　　　　　 (　　　)
A.a²－a　　　　　　B.(a－1)²　　　　　 C.(a²－1)　　　　　D.(a－)²

6.　　 在有穷数列{a_n}中，首项a₁＝1，末项a_n＝1997(n＞3)，若公差是自然数，则项数n的所有取值之和是　　　　　　　　　　　　　　　　　　　  　　　　　　(　　 )
A.3504　　　　　　 B.3501　　　　　　　C.1587　　　　　　　D.1997

二、填空题(共54分)

7.　　 用1和2这两种数字写n位数，其中任意相邻两位不全为1，记n位数的个数为f(n)，则f(10)＝________________.

8.　　 已知复数z₀，z₁，z₂，…，z_n，…满足z₀＝0，z₁＝1，z_n＋1－z_n＝α(z_n－z_n－1)，α＝1＋i，n＝1，2，…，则在圆z＝10的内部共含有z_n的个数为_____________.

9.　　 对满足不等式log₂p＜2的一切实数p中，使不等式x²＋px＋1＞3x＋p都成立的x的取值范围是_______________________.

10.　已知等腰梯形的最大边长为13，周长为28，面积为27，则它的最小边长为___________.

11.　若对非零常数m，函数f(x)满足f(x＋m)＋f(x－m)＝2f(x)cos(x∈R)，则f(x)是周期函数，它的一个周期是__________________.

12.　已知＜x＜2π，且cosxcos2x＝coscos，则x的取值为______________.

三、解答题(共计60分)

13.　(20分)用0，1，3，5，7五个数中任意不同的数作为一元二次方程的系数，问：
(1)可以作出多少个不同的一元二次方程？
(2)在这些方程中有实数根的有多少个？

14.　(20分)设S表示集合S中元素的个数，令n(S)表示包含空集及S自身在内的S的子集个数.如果A，B，C三个集合满足n(A)＋n(B)＋n(C)＝n(A∪B∪C)，A＝B＝100，那么A∩B∩C的最小可能值是多少？

15.　(20分)在平面上作一条直线，使得平面上三个已知点到这条直线的距离之和达到最小.

第二试

一、(50分)一次数学竞赛分一、二两试共有28个题目，每个参赛者都恰好解出7个题目，每两个题恰好有两名参赛者解出.试证：必有一个参赛者，他在第一试中或者一道也没有解出或者至少解出四道题.

二、(50分)如果一个矩形的长和宽都是奇数，在其内部是否存在这样的点，它到四个顶点的距离都是正整数.

三、(50分)若四面体的六条棱长分别为a，b，c，d，e，f，体积为V，求证：
a⁶＋b⁶＋c⁶＋d⁶＋e⁶＋f⁶≥432V².
其中等号当且仅当四面体为正四面体时取得.

全国高中数学联赛模拟试题(四)

参考答案

第一试

一、选择题

1.　　 B
x²＋bx≤－x(b＜－1) Þ 0≤x≤－(b＋1)
f(x)＝(x＋，当－(b＋1)≥－时，b≤－2
f(x)_min＝f(－ Þ b＝－＞－2矛盾.
－(b＋1)＜－时，－2＜b＜－1
f(x)_min＝f(－(b＋1))＝b＋1＝－

2.　　 C
可以验证①②③④⑥均成立，而令x＝时，⑤不成立.

3.　　 D
x₁与x₂共轭，设x₁＝r(cosθ＋isinθ)，则x₂＝r(cosθ－isinθ)
∴ ＝r(cos3θ＋isin3θ)∈R Þ θ＝
∴ ＝cos2θ＋isin2θ＝－i＝ω或ω²
当＝ω时 S＝1＋ω＋ω²＋ω⁴＋ω⁸＋……＋ω²¹⁹⁹⁵
　　注意到当n≥1时2ⁿ不是3的倍数，
∴ ω²ⁿ＝ω或ω²，于是ω^2n＋1＝ω^2×2n＝(ω²ⁿ)²＝ω²或ω
S中共计1997项，其中前三项和为0，以后的1994项每两项和为－1，∴ S＝－997
＝ω²时同理可得S＝－997

4.　　 C
可令A，B，C，D构成正四面体，O为其中心，则易得θ＝π－arccos

5.　　 D
令sinx＋cosx＝t∈[－]
则y＝(a＋
又因为a＞
所以 y≥(a－)²，当x＝时等号成立，
∴ y_min＝(a－)²

6.　　 B
a_n＝a₁＋(n－1)d
即(n－1)d＝1996＝4×499　(499为质数)
∴ n的所有取值之和为4＋499＋2×499＋4×499＝3501

二、填空题

7.144；
考虑数字末位数若为2，则有f(n－1)种，若为1，则第n－1位必为2，有f(n－2)种.
∴ f(n)＝f(n－1)＋f(n－2)且f(1)＝2，f(2)＝3

8.5；
z_n＋1－z_n＝α(z_n－z_n－1)＝α²(z_n－1－z_n－2)＝……＝αⁿ(z₁－z₀)＝αⁿ.
∴ z_n－z_n－1＝α^n－1，z_n－1－z_n－2＝α^n－2，……，z₁－z₀＝1
n个式子相加得z_n＝
当α＝1＋i时，解不等式z_n＜10，得n≤4
∴ n＝0，1，2，3，4共有5个

9.(－∞，，＋∞)；
解不等式log₂P＜2得＜P＜4
x²＋(p－3)x＋1－p＞0　Þ　x＞
转化为上式求最大值和最小值

10.5；
首先最大边不能为腰长，否则面积＜2×13×＜27
设下底长为13，上底长为x，则(13＋x)h×＝27
((13－x))²＋h²＝((15－x))²，解之得x＝5，则腰长为5，故最小边长为5.

11.7m；
可假设f(x)＝cosx，m＝，则可知7m＝2π为f(x)的一个周期.
不难验证7m是f(x)的一个周期.

12.{}
coscos＝cosxcos2x
令cosx＝t，则cos2x＝2t²－1
∴ 2t³－t－＝0，即(2t－1)(t²－)＝0
∴ t＝，相应的x＝

三、

13．(1)设所作一元二次方程为ax²＋bx＋c＝0，则a≠0
a有4种选择，b有4种选择，c有3种选择，共计有4×4×3＝48个不同的一元二次方程.
(2)考虑b的取值情况：
①b＝0时，方程不可能有实数根；
②b＝1时，只能取c＝0，a有三种可能，即有三个方程有实数根；
③b＝3时，只能取c＝0，a有三种可能，即有三个方程有实数根；
④b＝5时，取c＝0，a有三种可能；取c＝1，a＝3时有一种可能；取c＝3，a＝1时有一种可能.共计5个方程有实数根.
⑤b＝7时，取c＝0，a有三种可能；取c＝1时，a＝3或5有两种可能；取c＝3，a＝1有一种可能；取c＝5，a＝1时有一种可能；共计7个方程有实数根.
∴ 共有3＋3＋5＋7＝18个方程有实数根.

14．n(S)＝2^S，∴ n(A∪B∪C)＝2¹⁰⁰＋2¹⁰⁰＋n(C)
设A∪B∪C＝m·C＝P
则2^m＝2¹⁰¹＋2^p，2^p(2^m－p－1)＝2¹⁰¹
∴ 2^m－p－1＝1　Þ　m－p＝1
∴ m＝102，P＝101，即A∪B∪C＝102，C＝101
由容斥原理：A∩B∩C＝A＋B＋C－A∪B－B∪C－C∪A＋A∪B∪C≥97
当A∪C＝B∪C＝C∪A＝102时等号成立.
∴ A∩Β∩C_min＝97

15．(1)当三点在一条直线上时，所求直线就是经过三点的直线.
(2)若三点构成三角形，设为△ABC，其边长分别为a，b，c，并设a≥b≥c
如果直线不经过其中任何一点，如果三点在直线的同侧，则只需将直线向△ABC靠拢，直到直线经过最近的一个点，显然三点到直线的距离和在减小.
对于经过一个顶点的直线，将其绕这一点旋转，使其向经过这一点较长的一边靠拢，则另外两点到该直线的距离和也在减小，直到直线与这一边重合.
下面考虑直线与△ABC相交的情况，显然直线至少应该经过三点中的一个点，否则只需将直线向两点的一侧平移，距离和显然减小.而在三角形中，经过一顶点的直线被三角形截得的线段中，当线段与最长边重合时，长度最大，利用面积法可知，此时第三点到这条直线的距离就是所求最小值.
即所求直线为△ABC最长边所在的直线.

第二试

一、记题目组成的集合为X，参赛者组成的m元集合为Y，
若y_i解出题目x_j，就在y_i，x_j之间联一条线，
设点x_j次数为n，它与y₁，y₂，……，y_n相连，
则X中每一点恰与y_i相连(1≤i≤n)
∴ 2×27＝6n Þ n＝9
这个图共有28×9＝7m条边，∴ m＝36
设初试共有S道试题，解出1道，2道，3道试题的人数分别为α，β，γ，
若α＋β＋γ＝36，则α＋2β＋3γ＝9S，β＋C₃²γ＝2C_S²，
消去α、γ得β＝－2S²＋29S－108＜0，矛盾.
所以，必有一个参赛者，他在第一试中或者一道也没有解出或者至少解出四道题.

二、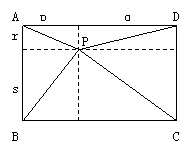假设存在这样的点P满足PA，PB，PC，PD均为整数，
过P作矩形各边的垂线，设长度分别为p，q，r，s.
且设p＋q＝a，r＋s＝b均为奇数，
PD²－PA²＝q²－p²＝(q－p)(q＋p)为整数，
可知p－q为有理数.
将矩形扩大p＋q倍，则p－q变为整数.
∴ p，q为的形式(m₁，n₁∈N)，同理，r，s为的形式(m₂，n₂∈N)
显然，m₁，n₁同奇偶，m₂，n₂同奇偶
若m₁，m₂同为奇，则由4(p²＋r²)≡2(mod 4)知p²＋r²不为完全平方数.矛盾.
∴ m₁，m₂铜为偶数，∴ p，q，r，s均为整数
又∵ p＋q＝a为奇数，r＋s＝b为奇数，
∴ p，q中有一个为奇数，不妨设为p，且r，s中有一个奇数，不妨设为r
则p²＋r²≡2(mod 4)不为完全平方数.矛盾.
所以，不存在满足条件的点.

三、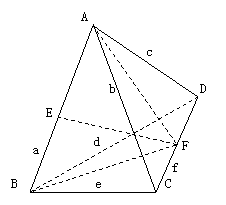取AB，CD的中点E，F，
则AF²＝(b²＋c²－f²)，BF²＝(d²＋e²－f²)
∴ EF²＝(b²＋c²＋d²＋e²－a²－f²)
V≤AB·EF·CD·
 ＝af
144V≤(b²＋c²＋d²＋e²－a²－f²)a²·f²
　　≤(b²＋c²＋d²＋e²－a²－f²)2a²·2f²
　　≤)³
　　≤2·()³
　　≤2·(幂平均不等式)
∴ a⁶＋b⁶＋c⁶＋d⁶＋e⁶＋f⁶≥432V².