全国高中数学联赛模拟试题(五)
第一试
一、选择题(共36分)
1.
由一个正方体的三个顶点所能构成的正三角形的个数为
( )
A.4 B.8 C.12 D.24
2.
在等比数列{an}中，记Sn＝a1＋a2＋……＋an，已知a5＝2S4＋3，a6＝2S5＋3，则此数列的公比为
( )
A.2 B.3 C.4 D.5
3.
在正n棱锥中，相邻两侧面所成的二面角的取值范围是
( )
A.(π，π) B.(π，π) C.(0，) D.(π)
4.
设函数f(x)对一切实数x都满足f(3＋x)＝f(3－x)且方程f(x)＝0恰有6个不同的实数根，这6个实数根的和为( )
A.0 B.9 C.12 D.18
5.
已知集合An＝{x2n＜x＜2n＋1，且x＝7m＋1，m，n∈N}，则A6中各元素之和为( )
A.792 B.890 C.891 D.990
6.
设(5＋7)2n＋1(n∈N)的整数部分和小数部分分别是I和F，则F·(I＋F)的值为( )
A.1 B.2 C.4 D.与n有关的数
二、填空题(共54分)
7. 若a＞0，a2－2ab＋c2＝0，bc＞a2，则实数a，b，c的大小关系为________________.
8. 正四面体ABCD的棱长为1，点G是底面△ABC的重心，点M在DG上，且使得∠AMB＝90º，则DM的长为_________________.
9. 二次方程(1－i)x2＋(λ＋i)x＋1＋iλ＝0(i为虚数单位，λ∈R)有两个虚根的充要条件是λ的取值范围为_______________________.
10. 已知有向线段PQ的起点P和终点Q的坐标分别为(－1，1)和(2，2)，若直线l:x＋my＋m＝0与PQ的延长线相交，则m的取值范围是_______________________.
11. 将一个四棱锥的每个顶点染上一种颜色，并使同一条棱的两端点异色，如果只有5种颜色可供使用，那么不同的染色方法种数为___________________.
12. 已知95个数a1，a2，……，a95，每个数都是＋1或者－1中的一个，那么它们的两两之积的和a1a2＋a1a3＋……＋a94a95的最小正值为________________.
三、解答题(共计60分)
13. (20分)数列{an}和{bn}满足a0＝b0＝1，an＝an－1＋2bn－1，bn＝an－1＋bn－1，(n＝1，2，……)，
求a22002－2b22002的值.
14. (20分)设a，b，c，d是四个不同的实数，使得＝4，且ac＝bd，求的最大值.
15. (20分)设0＜a＜b，过两定点A(a，0)和B(b，0)分别引直线l和m，使与抛物线y2＝x有四个不同的交点，当这四点共圆时，求这种直线l与m的交点的轨迹.
第二试
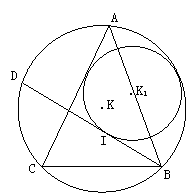一、(50分)△ABC内接于⊙K，BD是∠B的平分线，现有⊙K1与BD相切于点I，且与AC及⊙K也相切(如图)，证明切点Ｉ是△ABC的内心.
二、(50分)记F(x，y，z)是关于x，y，z的三次对称多项式，且每一项都是三次的，证明：
(1)当x，y，z≥0时，x(x－y)(x－z)＋y(y－x)(y－z)＋z(z－x)(z－y)≥0
(2)F(x，y，z)≥0对任意x，y，z≥0成立的充要条件是：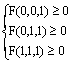
.
三、(50分)将重量为12，22，32，……，812的81个砝码分为三组，每组27个，并且各组重量相等.
全国高中数学联赛模拟试题(五)
参考答案
第一试
一、选择题
1. B
从正方体某一顶点出发的三条棱的另外三个端点恰好组成一个正三角形，因此正方体的每一个顶点“对应”一个正三角形，共计8个
2. B
a6－a5＝2(S5－S4)＝2a5，∴ a6＝3a5
∴ 公比q＝3
3. A
当n＝3时，θ＞，当n→∞时，θ→π
4. D
f(x)关于x＝3对称，每一对根之和为6，所以6个根之和为6×6÷2＝18
5. C
26＜7m＋1＜27，∴ 10≤m≤18
各元素和为(10＋11＋……＋18)×7＋9＝891
6. A
注意到(5＋7)2n＋1－(5－7)2n＋1∈N，且(5－7)2n＋1＜1
∴ F＝(5－7)2n＋1，
于是F·(I＋F)＝(5－7)2n＋1(5＋7)2n＋1＝1
二、填空题
7.b＞c＞a；
a2＋c2≥2ac Þ b≥c
若c≤a，则2ab＝a2＋c2≤2a2，
Þ b＜a Þ
bc＜a2，矛盾
∴ b≥c≥a，而等号显然不成立
8.；
设AB边的中点为E，则ME＝AB＝，∴ MG＝
而正四面体ABCD的高为，∴ DM＝
9.λ∈R且λ≠2；
整理方程得：(x2＋λx＋1)＋i(－x2＋x＋λ)＝0
若方程有实数根x，则x2＋λx＋1＝－x2＋x＋λ＝0
解得λ＝2，∴
λ≠2时方程两个根都是虚数.
10.(－)；
l恒过定点R(0，－1)，则可求得l得斜率取值范围是(，3)，即＜3
∴ m∈(－)
11.420；
分情况讨论.染5种颜色有P55＝120种，染4种颜色有：C51×C21×P43＝240种，染3种颜色有C52×P22×C31＝60种，共计420种.
12.13；
设有m个＋1，则有95－m个－1，
两两之积的和为S＝Cm2＋C
－m(95－m)＝2(m2－95m)＋47×95
最小正值为13，此时，m＝53或42
三、
13．直接计算得：
a20－2b20＝－1
a21－2b21＝1
a22－2b22＝－1
a23－2b23＝1
猜测：a2n－2b2n＝(－1)n＋1
下面用数学归纳法证明：
n＝0，1，2，3时，上面已经验证，猜测正确.
假设命题对n＝k成立，即a2k－2b2k＝(－1)k＋1
则当n＝k＋1时，
a2k＋1－2b2k＋1＝(ak＋2bk)2－2(ak＋bk)2
＝－(ak2－2bk2)＝(－1)k＋2
猜测正确
因此，根据数学归纳法，对任意的n∈Z，n≥0，猜测正确.
∴ a22002－2b22002＝－1
14．设a＝kb，d＝kc，则k＋＝4
令f＝，则f＝k
令x＝k＋，y＝，则x2≥4，y2≥4
x2y2＝f2，x＋y＝4 Þ x2＋y2＝16－2f
(x2－4)(y2－4)≥0 Þ f2－4(16－2f)＋16≥0 Þ y≥4或y≤－12
又∵ 如果同为正数，
则 ≥4 Þ a＝b＝c＝d，矛盾！
∴ a与c异号，b与d异号，于是f＜0
∴ fmax≤－12，等号在a＝1，b＝－1，c＝3＋2，d＝－3－2时可取到
∴ fmax＝－12
15．设P点(方程)坐标为P(x0，y0)，且设l与m的参数方程分别为
l:
分别代入抛物线方程中，得：
t2sin2α＋(2y0sinα－cosα)t＋y02－x0＝0
t2sin2β＋(2y0sinβ－cosβ)t＋y02－x0＝0
由四个交点共圆知： Þ
sin2α＝sin2β
显然，α≠β，则α＋β＝180°，∴ l，m关于x＝对称，
所以，交点P在x＝，但需除去点(，0)
即P点轨迹方程为x＝(y≠0)
第二试
一、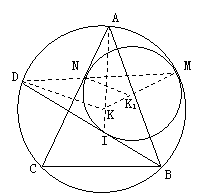
证明：设⊙K1切⊙K2于M，切AC于N，连结K，K1，M
则K，K1，M三点共线，
连结DK，DN，MN，AI
∵ K1N⊥AC，KD⊥AC，∴ NK1∥DK
又∵ △K1MN，△DKM均为等腰三角形
∴ D，N，M三点共线
则DI2＝DM·DN＝DA2
∴ DI＝DA
又∵ BD平分∠ABC
∴ I为△ABC的内心.
二、证明：⑴不妨设x≥y≥z≥0，令原式＝f(x，y，z)
则f(x，y，z)≥x(x－y)(y－z)＋y(y－x)(y－z)＋z(y－z)(x－z)
＝(y－z)(x2－xy＋y2－xy)＋z(y－z)(x－z)
＝(y－z)(x－y)2＋z(y－z)(x－z)
≥0
⑵设F(x，y，z)＝A(x3＋y3＋z3)＋B(x2y＋y2z＋z2x＋xy2＋yz2＋zx2)＋Cxyz
必要性是显然的
充分性：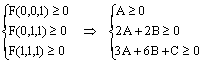
由⑴x3＋y3＋z3≥x2y＋y2z＋z2x＋xy2＋yz2＋zx2－3xyz
代入得
F(x，y，z)≥(A＋B)(x2y＋y2z＋z2x＋xy2＋yz2＋zx2)－3Axyz＋Cxyz
≥6(A＋B)xyz＋(C－3A)xyz
＝(3A＋6B＋C)xyz
≥0
充分性成立.
三、解：首先将重量为12，22，32，……，812的81个砝码分成9组，
每组9个，即Mn＝{(9n＋1)2，(9n＋2)2，……，(9n＋9)2n＝0，1，2，……，8}
再将每个Mn里面的9个砝码分成三组
(9n＋8)2 (9n＋1)2 (9n＋6)2
(9n＋3)2 (9n＋5)2 (9n＋7)2
(9n＋4)2 (9n＋9)2 (9n＋2)2
每一行为一组，和分别为Nn＋a，Nn＋b，Nn＋c，其中，a，b，c与n无关，
然后，再将27个小组并为3组，每9组并为一大组：
N1＋a，N2＋a，N3＋a，N4＋b，N5＋b，N6＋b，N7＋c，N8＋c，N9＋c，
N1＋b，N2＋b，N3＋b，N4＋c，N5＋c，N6＋c，N7＋a，N8＋a，N9＋a，
N1＋c，N2＋c，N3＋c，N4＋a，N5＋a，N6＋a，N7＋b，N8＋b，N9＋b.
显然各组的总重量均为
＋3(a＋b＋c)，并且每组27个砝码.