试卷类型：A
高中调研测试题高三数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试时间120分钟．
第 Ⅰ 卷 (选择题，共60分)
注意事项：
1．请考生将自己的姓名、学号、班级填写在第Ⅱ卷密封线内．
2．每小题选出答案后在第Ⅱ卷前的答题栏内用铅笔把对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案．
|
|
一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1.
已知集合A、B，则“A
B”是“A∩B＝A”的
A．充分而不必要条件 B．必要而不充分条件
C．充要条件 D．既不充分也不必要条件
2.
过点C (1，2)作直线，使其在坐标轴上的截距相等，则满足条件的直线的斜率为
A．－1 B．±1 C．－1或2 D．±1或2
3.
下列命题中，正确的是
A．两个单位向量的数量积为1 B．若a·b＝a·c，且a≠0；则b＝c
C．若b⊥c，则(a＋c)·b＝a·b D．若9a2＝4b2，则3a＝2b
4.
将函数
按向量a＝(
，1)平移后的解析式是
A．
B．
C．
D．
5.
(理科考生做)已知不等式x－2≤
的解集为{x｜x≤－1或0＜x≤3}，则实数a等于
A．－3 B．－1 C．1 D．3
(文科考生做)已知方程
有一个根大于1，而另一个根小于1，则实数
的取值范围是
A．(－∞，1)∪(9，＋∞) B．(1，9)
C．(－∞，1) D．[1，＋∞)
6.
长方体的一个顶点上的三条棱长分别为1，2，3，该长方体的顶点都在同一个球面上，则这个球的半径为
A．
B．
C．
D．
7. 若函数f (x)
(x∈R)是奇函数，且是周期函数，a是它的一个周期(a≠0)，则
＝
A．
a B．－a C．
D．0
8. 已知直线l⊥平面
，直线
平面
，以下四个命题：①
；②
；③
；④
．
其中真命题是
A．①② B．③④ C．①③ D．②④
9. 已知双曲线的中心在原点，两个焦点为F1 (－
，0)和F2 (，0)，P在双曲线上，满足
＝0且△F1PF2的面积为1，则此双曲线的方程是
A．
B．
C．
D．
10. (理科考生做)下面说法正确的是
A．离散型随机变量x 的期望Ex 反映了x 取值的概率的平均值
B．离散型随机变量x 的方差Dx 反映了x 取值的平均水平
C．离散型随机变量x 的期望Ex 反映了x 取值的平均水平
D．离散型随机变量x 的方差Dx 反映了x 取值的概率的平均值
(文科考生做)要完成下列2项调查：①从某社区125户高收入家庭，280户中等收入家庭，95户低收入家庭中选出100户调查社会购买力的某项指标；②从某中学高一年级的12名体育特长生中选出3人调查学习负担情况。应采用的抽样方法是
A．①用随机抽样法 ②用系统抽样法 B．①用分层抽样法 ②用随机抽样法
C．①用系统抽样法 ②用分层抽样法 D．①、②都用分层抽样法
11. 不等式
的解集为
A．｛xïx＞－1｝ B．｛xïx＜1｝ C．｛xïx＜2｝ D．｛xï－1＜x＜2｝
|
|
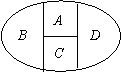
12. 用6种不同的颜色给图中A、B、C、D四块区域涂色，允许同一色涂不同的区域，但相邻的区域不能涂同一色，则不同的涂法共有
A．400种 B．460种
C．480种 D．496种
第Ⅰ卷答题栏
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||
[ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | ||||
[ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | ||||
[ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | ||||
| [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] |
调研测试题
高 三 数 学
第 Ⅱ 卷 (非选择题，共90分)
注意事项：
第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 29 | 21 | 22 | ||||
| 得 分 | |||||||||
| 得分 | 评卷人 |
二．填空题：本大题共4小题，每小题4分，共16分。将正确答案填在题中横线上．
13. (理科考生做)设z＝1＋
i，则
＝ ．
(文科考生做)等差数列{an}中，若a1＋a4＋a7＝15，a3＋a6＋a9＝3，则S9＝ ．
14. 
的展开式的第4项是
.
15. 已知圆x2＋y2＋mx－
＝0与抛物线y＝x2的准线相切，则m= .
16. (理科考生做)关于函数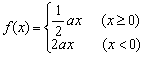
(a是常数且a≠0)，给出下列命题：①它是一个奇函数；②它在每一点都连续；③它在每一点都可导；④它是一个增函数；⑤它有反函数．其中不正确的命题序号是 ．
(文科考生做)已知函数f (x)＝｜x2－2ax＋b｜(x∈R)．给出下列命题：①f (x)必是偶函数； ②当f (0)＝f (2)时，f (x)的图象关于直线x＝1对称； ③若a2－b≤0，则f (x) 在区间[a，＋∞)上是增函数；④f (x)有最大值｜a2－b｜．其中正确命题的序号是 ．
三．解答题：本大题共6小题，满分74分．
| 得分 | 评卷人 |
17.
(本大题满分12分)△ABC中，sin A cos2 
+ sin C cos2 
=
sin B , 求角B的范围．
| 得分 | 评卷人 |
18.
(本大题满分12分) 已知f (x)＝x3＋ax2＋bx＋c在x＝
与x＝1时，都取得极值．
(1)求a、b的值；
(2)若对x∈[－1，2]，f (x)＜c2恒成立，求c的取值范围．
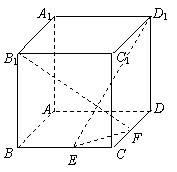
19. (本大题满分12分) 在棱长为a的正方体ABCD－A1B1C1D1中，E、F分别是棱BC、CD上的点，且BE＝CF．
|
|
(1)求证：B1F⊥D1E；
(2)当三棱锥C1－CEF的体积取得最大值时，求二面角C1－EF－C的大小．
| 得分 | 评卷人 |
20.
(本大题满分12分)
(理科考生做) 某保险公司新开设了一项保险业务，若在一年内事件E发生，该公司要赔偿a元．设在一年内E发生的概率为p，为使公司收益的期望值等于a的百分之十，公司应要求顾客交多少保险金？
(文科考生做)有一批食品出厂前要进行五项指标检验，如果有两项指标不合格，则这批食品不能出厂．已知每项指标抽检是相互独立的，且每项抽检出现不合格的概率都是0.2．
(1)求这批产品不能出厂的概率(保留三位有效数字)；
(2)求直至五项指标全部验完毕，才能确定该批食品是否出厂的概率(保留三位有效数字)．
| 得分 | 评卷人 |
21.
(本大题满分12分)
(理科考生做) 设
，定义
，其中n∈N*．
(1)求数列{an}的通项公式；
(2)若T2n＝a1＋2a2＋3a3＋……＋2na2n，
(n∈N*)，试比较9T2n与Qn的大小，并说明理由．
(文科考生做)已知函数f (x)＝(x－1)2，数列{an}是公差为d的等差数列，{bn}是公比为q (q∈R且q≠1)的等比数列，若a1＝f (d－1)，a3＝f (d＋1)，b1＝f (q＋1)，b3＝f (q－1)．
(1)求数列{an}和{bn}的通项公式；
(2)设数列{cn}的前n项和为Sn，且对一切自然数n均有：
成立，求
．
| 得分 | 评卷人 |
22.
(本大题满分14分)
(理科考生做)已知二次函数f (x)＝ax2＋bx＋c(a＞0)的图象与x轴有两个不同的公共点，若f (c)＝0，且0＜x＜c时，f (x)＞0．
| 得分 | 评卷人 |
(1)试比较
与c的大小；
(2)证明：－2＜b＜－1；
(3)当c＞1，t＞0时，求证：
＞0．
(文科考生做)已知奇函数f (x)的定义域为(－∞，0)∪(0，＋∞)，且f (x)在(0，＋∞)上是增函数，f (1)＝0，函数g (x)＝－x2＋mx＋1－2m，x∈[0，1]．
(1)证明函数f (x)在(－∞，0)上是增函数；
(2)解关于x的不等式f (x)＜0；
(3)当x∈[0，1]时，求使得g (x)＜0且f [g
(x)]＜0恒成立的m的取值范围．