高中高三月考（Ⅱ）数学试题
第Ⅰ卷
一、选择题（本题共12小题，每小题5分，共60分）
1．若命题“非p”与命题“p或q”都是真命题，那么
A．命题p与命题q的真值相同 B．命题q一定是真命题
C．命题q不一定是真命题 D．命题p不一定是真命题
2．下列四个函数中，在区间（0，1）上为增函数的是
A．
B．
C．
D．
3把函数
的图像按向量
经过一次平以后得到
的图像，则为
A．(2,
) B．
C．
D．
4．若0为平行四边形ABCD的中心，
等于
A．
B．
C．
D．
5．在等比数列
A．
B．
C．
D．
6．已知集合
则M中只含二个元素的子集的个数为（ ）
A．3 B．15 C．21 D．42
7．函数
的最大值是
A．
B．
C．3 D．2
8．设
、
是平面直角坐标系内
轴、
轴正方向的两个单位向量，且向量
， 
，
，则四边形
的面积是
9．已知
则不等式
A．
B．
C．
D．
10．命题p：若
，则
；命题q：若
，则
。那么命题p与命题q的关系是
A．互逆 B．互否 C．互为逆否命题 D．不能确定
11．设偶函数
的大小关系是
A．
B．
C．
D．不能确定
12．设函数f (x)的定义域为D，如果对于任意的
，使
成立，则称函数f (x)在D上均值为C，给出下列四个函数
①
②
③
④
则满足在其定义域上均值为2的所有函数是
A．①② B．③④ C．②④ D．①③
高中高三月考（Ⅱ）
数学试题
第Ⅱ卷
二、填空题（本题共4小题，每小题4分，共16分）
13等差数列
的前n项和为Sn,且
如果存在正整数M，使得对一切正整数n，
都成立.则M的最小值是
14．已知数列
满足：
，则使
成立的n的值是 ．
15．已知
.
16.今有下列命题：
①函数
在第一象限是增函数；
②函数
是偶函数；
③函数
的一条对称轴是
；
④函数
的对称轴
是
，则
；则其中正确的命题有
。
高三月考（Ⅱ）
数学试题 答题纸
二、填空题 13 14 15 16
三、解答题：（本大题共6小题，共74分）
17． （12分）已知
，
，且
，
，求
的值。
18．
（12分）已知函数
，若
，且
，求实数
的取值范围。
19.（12分）设
、
、
均为非零向量，其中任意两个向量不平行，若与
平行，与
平行，求证：
。
20．（本题满分12分） 设函数
…，是公差为2的等差数列，且x1=a4
（1）求数列
的通项公式；（2）
；
（3）令
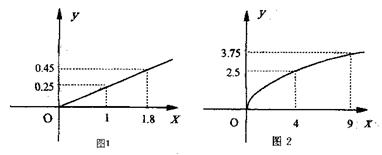
21．（本题满分12分）某民营企业生产A、B两种产品，根据市场调查与预测，A产品
的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其
关系如图2（注：利润与投资单位：万元）
（1）分别将A、B两种产品的利润表示为投资的函数关系式写出
（2）该企业已筹集到10万元资金，并全部投入A、B两种产品的生产，问：怎样分配这10万元投资，才能使企业获得最大利润，其最大利润约为多少万元（精确到1万元）
|
22．（本题满分12分）设各项均为正数的数列
的前n项和为
，对于任意的正整数n都有等式
成立.
（Ⅰ）求
；
（Ⅱ）求证
;
（III）求
.