高考专题卷：立体几何测验（1）
班级_______ 学号_____________ 姓名_____________
一． 选择题：（6×7=42分）
1．下列四个命题中，其本身与其逆命题都成立的是（ ）
A．正四棱柱一定是长方体 B．正方体一定是正四棱柱
C．直平行六面体一定是直四棱柱 D．侧棱与底面垂直的棱柱是直棱柱
2．一个四棱锥的所有侧面与底面所成的角都是30°，若此棱锥的底面面积为S，则它的侧面面积等于（ ）
A．
B．
C．
D．2S
3．四面体的一条棱长是x,其余棱长都是1，则该四面体的体积最大时，x的值为（ ）
A．
B．2
C．
D．
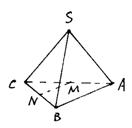
4．正三棱锥S－ABC的底面边长为a，侧棱长为b，M
为AC的中点，N为BC的中点，过MN平行于SC的
平面在正三棱锥内的截面面积为（ ）
A．
B．
C．
D．
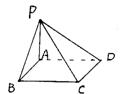
5．过正方形ABCD的顶点A，引PA⊥平面ABCD，
若PA=AB，则平面ABP和平面CDP所成的二面角
的大小是（ ）
A．30° B．45°
C．60° D．90°
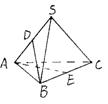6．设三棱锥S－ABC中，SA、S B、SC两两垂直，
且SA=4，SB=3，SC=5，D为SA的中点，E为BC
的中点，则三棱锥B－AED的体积等于（ ）
A．
B．
C．5 D．10
二． 填空题（4×7=28分）
7．三棱锥S－ABC中，SA、SB、SC两两垂直，则S在平面ABC上的射影为△ABC的________心。
8．若P－ABCDEF为正六棱锥，则∠APB的取值范围为____________。
9．过棱锥高的三等分点作两个平行于底面的截面，它将棱锥的侧面分成三部分面积之比（从上到下）为_____________.
10．三棱锥S－ABC中，SC=AB=1，SA与BC中点分别为P、Q，且PQ=
，则异面直线AB与SC所成的角为___________.
三． 解答题：
11．（15分）在底面为等腰直角三角形的直三棱柱ABC－A1B1C1中，∠ACB=90°，AC=BC=A1A。
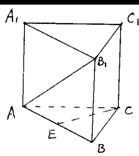(I) 求AB1与BC1所成的角；
(II) 若点E为AB的中点，求CE与BC1所成的角；
(III) 求二面角A1－AB1－C1的大小
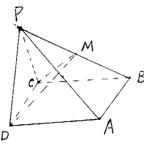
12．（15分）如图，在棱锥P－ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，且∠ADC=60°，M为PB的中点。
(I) 求证：PA⊥CD；
(II) 求二面角P－AB－D的大小；
(III) 求证：平面CDM⊥平面PAB。
【参考答案】
一、1．D 2.C 3.D 4.A 5.B 6.A
二、7.垂 8.（0,
）
9.1:3:5
10. 90°
三、11．（1）连结B1C交BC1于O，取AC中点D，连结OD可得∠BOD=90°，AB1与BC1成90°角.
（2）取A1B1中点F，连结C1F、BF，可得∠BC1F=60°，CE与BC1所成角60°.
（3）在平面A1B中作FH⊥AB1于H，连结C、H，
可证∠C1HF为二面角的平面角∠C1HF=60°.
12．（1）取CD中点E，连结PE、AE、AC可证CD⊥平面PEA。
（2）可证∠PAE为二面角的平面角.∠PAE=45°.
(3)取PA中点G，连结GD、MG可证PA⊥平面CDGM.