立体几何测验（2）

高考专题卷：立体几何测验（2）

班级_______学号___________姓名_________

一．　　　　　　 选择题（6×7=42分）

1．以三棱锥各面重心为顶点得到一个新三棱锥，则它的表面积是原三棱锥表面积的（　　）

A．　　　　B．　　　 C．　　  　D．

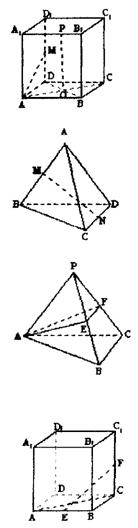2．侧棱长为的正三棱锥V－ABC的侧棱间的夹角都为40°，过顶点A作截面AEF，则截面AEF的最小周长为（　　　）

A．2　　　 B．3　　　　 C．6　　　　D．6

3．在四面体的六条棱中，相互垂直的棱至多有（　　 ）

A．3对　　 　B．4对　　 　C．5对　　　D．6对

4．在正方体ABCD－A₁B₁C₁D₁中，M是棱DD₁的中点，

O为底面ABCD的中心，P为棱A₁B₁上的任一点，则直

线OP与AM所成的角等于（　　）

A．30°　　　　 B．60°　　　　

C．90°　 　　　D．不能确定

5．三棱锥A－BCD中，AD=BC，M、N分别为AB、

CD的中点，以MN与AD成30°角，则AD与BC

所成角为（　　）

A．30°　　　　  B．120°　　　　

C．60°　　　　  D．90°

6．正三棱锥P－ABC中，E、F是侧棱PB、PC的中点，

若截面AEF垂直于侧面PBC，则棱锥的侧面积与底面积

之比为（　　）

A．　　　 B．　　　 C．　　  D．

二．　　　　　　 填空题：（4×7=28分）

7．三棱锥S－ABC中，SA、SB、SC两两垂直，且SA=5，SB=4，SC=3，则SA与BC间的距离等于___________.

8.正方体ABCD－A₁B₁C₁D₁中，E、F分别是棱AB、CC₁的中点，则异面直线AC与EF所成角的余弦值为________。

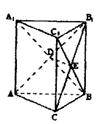9．已知斜棱柱直截面周长为8，高为4，侧棱与底面成60°角，则斜棱柱侧面积是_________。

10．如图，直三棱柱ABC－A₁B₁C₁的侧棱和底面边长都是a，截面AB₁C与截面A₁BC₁相交于DE，四面体BB₁DE的体积为_________。

三．　　　　　　 解答题：

11．（12分）如图，在长方体ABCD－A₁B₁C₁D₁中，棱长AB=，AA=1，截面ABC₁D₁为正方形。

（I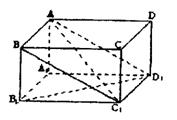）　　　　　　　　　  求直线B₁D₁与平面ABC₁D₁所成角的大小；

（II）　　　　　　　　 求二面角B－AC₁－B₁的大小。

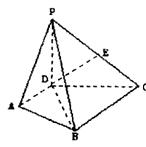12．（18分）如图，在四棱锥P－ABCD中，PD⊥平面ABCD，AD⊥DC，AD∥BC，PD=DC=1，BC=

(I)　　　　　　　　 求PB与平面PDC所成角的大小；

(II)　　　　　　  求二面角D－PB－C的大小；

(III)　　　　　  若AD=BC，E为PC中点，求证：DE∥平面PAB。

【参考答案】

一、1．C　　 2.C　　3.D　 4.C　 5.C　 6.D

二、7.　　 8.　　9.　　 10.

三、11．(1)在平面B₁C内，作B₁H⊥BC₁于H，连结D₁H可证B₁H⊥平面ABC₁D₁，∠B₁D₁H即为所求，∠B₁D₁H=arcsin.

(2)过H作HK⊥AC₁于K，连结B₁K、AB₁可证∠HKB₁即为所求∠HKB₁=45°

12.（1）可证BC⊥平面PDC　　 ∠BPC即为所求，∠BPC=45°

（2）∠Rt△PBD中，过D作DH⊥PB于H. 取PB中点G . 连结CG，CG⊥PB.

可证∠DHE即为所求. ∠DHE=arccos.

(3)取PB中点F，连结EF，AF. 可证EF　 AD，得　EFAD.

DE∥AF，因此DE∥平面PAB。