普通高中毕业班数学综合测试（一）

普通高中毕业班数学综合测试（一）

　　　　数　　  学

本试卷分第I卷（选择题）和第II卷（非选择题）两部分。第I卷第1至

2页。第II卷3至8页。共150分。考试时间120分钟。

第I卷（选择题共60分）

注意事项

1．　答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写

在答题卡上。

2．　每小题选出答案后，用铅笔把答题卡对应题目的答案标号涂黑，如需改

动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3．　考试结束，监考人将本试卷和答题卡一并收回。

参考公式：

三角函数和差化积公式

正棱台、圆台的侧面积公式

其中、分别表示上、下底面周长，表示斜高或母线长

台体的体积公式

其中、分别表示上、下底面积，表示高

一、选择题:本大题共12小题，每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.

1.　　　  设全集I=R,M=｛xlg()=lgx｝,N=｛x｝,则集合等于（　 ）

A.｛2｝  　　　　　　　　　　　　　　　　　　　　　 B.｛｝

C.｛｝　　　　　　　　　　　　　　　  D.｛｝

2.　　　  函数的图象大致是（　　　　）　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　A　　　　　　　　　　　　B　　　　　　　　　　C　　　　　　　　　　　D

3.　　　  若抛物线与抛物线有公共焦点，则

A．2h=p-q　　　  B.2h=p+q　　　　 c.2h=-(p+q)　　　 D.2h=-(p-q)

4.　　　  在的展开式中的系数为

A．-6　　　　  B.-4　　　　　 C.4　　　　　　　 D.6

5.　　　  在正三棱台中，二面角等于，则侧棱与下底面ABC所成的角为

A．　　  B.　　　　 C.　　　　　　　D.

6.　　　  复数的辐角主值为

A．　　　　　 B.　　　　　　　　　　　

7.　　　  函数的最大值为

A．4　　　　　　 B.　 　　　　　　　　　C.6　　　　　　  D.

8.　　　  在母线长为2的等边圆锥内作一个内接圆柱，当这个圆柱的侧面积最大时，圆柱的高是

A．　　　　　　　B．　　　　　　　　Ｃ．　　　　　　Ｄ．

9.　　　  设定义在R上的一个减函数，，那么必为

A．增函数且是奇函数　　　　　　　　　　　 　　B. 增函数且是偶函数

C. 减函数且是奇函数　　　　　　　　　　　　　 D. 减函数且是偶函数

10.　　 设双曲线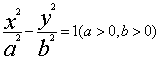的右准线与两渐近线交于A,B两点，点F为右焦点，若以AB为直径的圆经过点F,则该双曲线的离心率为

A.　　　　　　　　B.2　　　　　　　　  C.　　　　　　　　　 D.

11.　　 已知点M(a,b)(ab0)是圆C：内一点，直线是以M为中点的弦所在的直线，直线的方程是,那么

A． 　　　　 B.

C．　　　　　D.

12.　　 甲烷分子由一个碳原子和四个氢原子组成，其空间构型为一正四面体，碳原子位于该正四面体的中心，四个氢原子分别位于该正四面体的四个顶点上，若将碳原子和氢原子均视为一个点(体积忽略不计)，且已知碳原子每个氢原子间的距离都为a，则以四个氢原子为顶点的这个正四面体的体积为

A．　　　　　B.　　　　　C.　　　　　　　 D.

普通高中毕业班综合测试(一)

　　　 　　　　　　　　　数　　学

　　　　　　　　   第II卷（非选择题共90分）

注意事项：

1．第II卷共6页，用钢笔或圆珠笔直接写答在试题卷中。

2．答卷前将密封线内的项目填写清楚。

二．填空题：本大题共4小题；每小题4分，共16分，把答案填在题中横线上。

13.　　 如果椭圆的对称轴为坐标轴，焦点在x轴上，由短轴的一端点与两焦点连结而成的三角形是等边三角形，且,那么椭圆的方程是　　　　　　　　　　　　　　　  　　

14.　　 某市拟成立一个由6名大学生组成的社会调查小组，并准备将这6个名额分配给本市的3所大学，要求每所大学都有学生参加，则不同的分配方法共有　　　　　　  种(用数字作答)

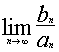15.　　 设数列的前n项和，其中数列是公差为2等差数列且则的值为　

　　　　　　　　　　　　　　　　　　　　　　　　　

16.　　 设是不重合的两条直线，是不重合的两个平面，给出下列命题：

①②

③④

其中正确命题的序号是　　　　　　　　　.（注：把你认为正确的命题的序号都填上）

三、解答题：本大题共6小题；共74分，解答应写出文字说明、证明过程或演算步骤

17.　　(本小题满分12分)

已知a>0,且a1,解关于x的不等式

　　　　　　

18.　　 (本小题满分12分)

在中，三个内角A，B，C的对边分别为a,b,c,且角A为，，求角C的度数。

19.　　 (本小题满分12分)

如图，在三棱锥A－BCD中，AB，BC，CD两两垂直。　　　　　　　　 A

⑴由该棱锥所有的两个面组成的二面角中，哪些是直二面角？

（要求全部写出，并说明理由）。

⑵若AD与平面BCD所成的角为，AD与平面ABC所成的角为，　B　　　　　　　　　　 D

求二面角B－AD－C的余弦值；

⑶若AD与平面BCD所成的角为，AD与平面ABC所成的角为，且AD＝6　　　　　　　　C

则当、为何值时，三棱锥A－BCD的体积最大，最大值是多少？

20.　　 (本小题满分12分)

已知a,b,c,.

⑴若a+c=0,上最大值为2，最小值为，证明：；

⑵若a>0,p，q是满足p+q=1的实数，且对任意的实数x,y均有

，证明：。

21.　　 (本小题满分12分)

某种果树至少要培植五年才开始采果，有一农户于1998年初利用边角地种植了一些这种果树，1993年开始采果，当年的产量为156千克，1994年至1998年，连续5年每年的产量平均比上一年增加50﹪还多34千克从1999年起，由于管理等方面的原因导致产量开始下降，且平均每年比上一年减少10﹪，据估计这种情况还会继续下去。

⑴1998年，该农户采得这种水果多少千克？

 ⑵如果用表示该农户从1993年起的n()年内采得这种水果的总量，试求出用n表示的的表达式，并据此计算，到2000年底，该农户共采得这种水果多少千克？(精确到1千克)

22.　　 (本小题满分12分)

已知抛物线的焦点为F，准线为，是否存在双曲线C，同时满足以下两个条件：

⑴双曲线C的一个焦点为F，相应于F的准线为

⑵双曲线C截与直线x-y=0和垂直的直线所得线段AB的长为，并且线段AB的中点恰好在直线x-y=0上。

　若存在，求出该双曲线C的方程；若不存在，说明理由。