上学期高三年级数学科月考试卷参考答案
一. 选择题（本题共36 分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | A | A | C | B | B | B | D | D | D | C |
二、填空题（本题共16分）
13.
14.
15.①③④ 16.
三、解答题（本题共48分）
17.解：
（1）依题意知
………①
…………
又
∴
………②………………………
从而
………③……………………………………
把②③代入①得
即
∴
一定为等差数列………………………………………………
（2）又
代入①得
把，
代入②
得
从而知的公差
……………………………
∴
……………………………………
∴
（n=1时也成立）………
∴
…
18.解：
法一：原式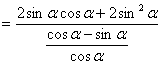
……………………………
又
两边平方得
∴
……………………………………………………
又
∴
…………
∴
………………………………
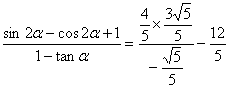法二：两边平方得
∴
……………………………………………
又∴……………
∴
………………………
从而得到
∴
………………………
∴
………………………
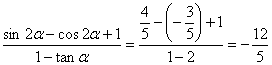19.解：
（1）
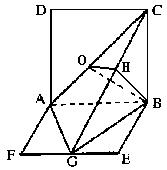依题意知
从而有
又
…………………
又面ABCD⊥面ABEF且BC⊥AB
∴BC⊥面BGC…………………
∴AG⊥BC∴AG⊥面BGC
∴面AGC⊥面BGC…………………
（2）过B作BH⊥GC于H∵面AGC⊥面BGC∴BH⊥面AGC………
∴∠BGH为所求角，在RT△CBG中，
……
（3）取AC中点O连结BO则BO⊥AC又BH⊥面AGC∴HO⊥AC
∴∠BOH为所求平面角的二面角………………………………………
又
∴在RT△BHO中，
∴
………………………………………………
20.证明：
（1）设第n年该乡从两企业获得利润为y万元。
……………………………………………
………………………………………………
当且仅当
时，即
时
故1993年获得利润最小，…………………………………………………
为解决温饱问题需另筹集2000-960=1040（万元）………………………
（2）令n=9，
………………………………
能达到小康水平。……
21.解：
（1）设动圆圆心为
，定圆的圆心
，半径r=4…………
则
…………………………………………………………
由椭圆的定义知动圆圆心的轨迹方程为
……………………
（2）设动圆圆心为，定圆的圆心
半径r=2…………
则
………………………………………………………
由双曲线的定义知动圆圆心的轨迹方程为
………………
22.证明：
（1）
…………………
………………………………
Ⅰ）当
即
时，
则
时，
……………………………
Ⅱ）当
即
时，
则
时，
……………
Ⅲ）当
即
时，
则
时，
………………………
综上所述得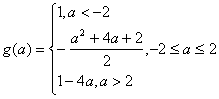
……………
（2）令
得
，
或
（舍去）
（∵
）；再令
（舍去）（∵
）
∴…………………………………………………………………
当时，
∴当时，
……………………………………