上学期高三期中测试数学试题
第I卷
参考公式: 球的表面积公式
如果事件A、B互斥,那么
![]()
P(A+B)=P(A)+P(B) 其中R表示球的半径
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B) 球的体积公式
|
是P,那么n次独立重复试验中恰好发生k
|
![]()
一、选择题:本大题共12小题;每小题5分,满分60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列集合恰有2个元素的集合是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
|
|
3. 已知随机变量![]() 满足E
满足E![]() =2,则E(2
=2,则E(2![]() +3)= ( )
+3)= ( )
A.4 B.8 C.7 D.5
4.已知 a =2 sin15°, b =4 cos15°,a与b的夹角为30°,则a·b为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.不等式![]() 的解集为 ( )
的解集为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.函数y=sin2x+2cosx(![]() )的最大值与最小值分别为 ( )
)的最大值与最小值分别为 ( )
A.最大值![]() ,最小值为-
,最小值为-![]() B.最大值为
B.最大值为![]() ,最小值为-2
,最小值为-2
C.最大值为2,最小值为-![]() D.最大值为2,最小值为-2
D.最大值为2,最小值为-2
7.已知![]() ,且
,且![]() ,则 z 的取值范围是 ( )
,则 z 的取值范围是 ( )
A.[0,2] B.[1,3] C.[0,3] D.[1,2]
8.当![]() 的值为 ( )
的值为 ( )
A.1 B.-1 C.i D.-i
9.![]() 是定义在R上,以2为周期的偶函数,当
是定义在R上,以2为周期的偶函数,当![]() 时,
时,
![]() 的表达式为 ( )
的表达式为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.对一切实数x,函数![]() 恒为正值,则实数a的取值范围是
恒为正值,则实数a的取值范围是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.函数![]() 上是增函数,则数p的取值范围是 ( )
上是增函数,则数p的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
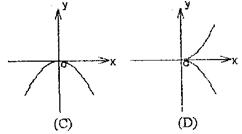
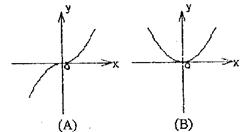
12.下面四个判断中,正确的是 ( )
A.![]()
B.![]()
C.![]()
D.![]()
![]() ,
,
则![]()
二、填空题:本大题共4小题;每小题4分,满分16分。
13.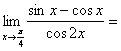 .
.
14.函数![]() 的图象按向量a 平移后,所得函数的解析式是
的图象按向量a 平移后,所得函数的解析式是![]() ,则a等于
.(只需写出满足条件的一个向量)
,则a等于
.(只需写出满足条件的一个向量)
15.与函数![]() 的图象相切,切线斜率为1的切线方程是
.
的图象相切,切线斜率为1的切线方程是
.
16.有下列四个命题:
①“若xy=1,则x、y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若![]() 有实根”;
有实根”;
④“若![]() ”的逆否命题.
”的逆否命题.
其中真命题为 .
三、解答答:本大题共6小题;共74分。解应写出文字说明、证明过程或演算步骤。
17.(满分12分)已知![]() 的值.
的值.
18.(满分12分)一名学生骑自行车上学,从他的家到学校的途中有6个交通岗,假设他在各交通岗遇到红灯的事件是独立的,并且概率都是![]() .
.
(I)求这名学生首次遇到红灯前,已经过了两个交通岗的概率;
(II)求这名学生在途中遇到红灯数![]() 的期望与方差.
的期望与方差.
19.(满分12分)已知平面上三个向量a、b、c的模均为1,它们相互之间的夹角均为
120°
(I)求证:(a-b)⊥c;
(II)若ka+b+c>1(k∈R),求k的取值范围.
20.(满分12分)已知函数![]() 是奇函数,正数数列{
是奇函数,正数数列{![]() }满足
}满足![]()
(I)求{![]() }的通项公式;
}的通项公式;
(II)若{![]() }的前n项和为
}的前n项和为![]() .
.
21.(满分12分)某农产品去年各季度的市场价格如下表:
| 季 度 | 第一季度 | 第二季度 | 第三季度 | 第四季度 |
| 每吨售价 (单位:元) | 195.5 | 200.5 | 204.5 | 199.5 |
今年某公司计划按去年各季度市场价格的“平衡价m”(平衡价m是这样的一个量:m与各季度售价差的平方和最小)收购该种农产品,并按每个100元纳税10元(又称征税率为10个百分点),计划可收购a万吨,政府为了鼓励公司多收购这种农产品,决定将税率降低x个百分点,预测收购量可增加2x个百分点,
(I)根据题中条件填空,m= (元/吨);
(II)写出税收y(万元)与x的函数关系式;
(III)若要使此项税收在税率调节后不少于原计划税收的83.2%,试确定x的取值范围.
22.(满分14分)已知函数![]() 在区间[0,1]单调递增,在区间
在区间[0,1]单调递增,在区间![]() 单调递减,
单调递减,
(I)求a的值;
(II)若点![]() 的图象上,求证点A关于直线
的图象上,求证点A关于直线![]() 的对称点B也
的对称点B也
在函数![]() 的图象上;
的图象上;
(III)是否存在实数b,使得函数![]() 的图象与函数
的图象与函数![]() 的图象恰有3个交
的图象恰有3个交
点,若存在,请求出实数b的值;若不存在,试说明理由.
参考答案
一、BACBCB BDDDAC
二、13.![]() 14.
14.![]() (
(![]() ) 15.
) 15.![]() 16.①②③
16.①②③
三、
17.解:由条件,![]() …………………………………………2分
…………………………………………2分
![]()
![]() ………………………………4分
………………………………4分
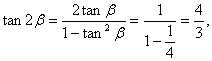 …………………………………………6分
…………………………………………6分
![]() ……………………………………………………8分
……………………………………………………8分
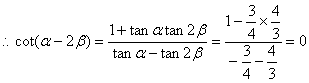 ………………………12分
………………………12分
18.解:(I)![]() …………………………………………4分
…………………………………………4分
(II)依题意![]() ~
~![]() ……………………………………………………7分
……………………………………………………7分
![]() ……………………………………………………………9分
……………………………………………………………9分
![]() ……………………………………………………12分
……………………………………………………12分
19.解:(I)![]() a、b、c之间的夹角均为120°,
a、b、c之间的夹角均为120°,
![]() …3分
…3分
![]()
(II)![]()
![]() …………………………………6分
…………………………………6分
![]() ……………………………………………8分
……………………………………………8分
![]() ………………………………………………………………………10分
………………………………………………………………………10分
![]() ……………………………………………………………………12分
……………………………………………………………………12分
20.解:(I)![]() 为偶函数,
为偶函数,
![]() ………………………………………2分
………………………………………2分
![]() 为奇函数,
为奇函数,
![]() ………………………………………………4分
………………………………………………4分
![]() …5分
…5分
![]()
![]() ……………………………………………………7分
……………………………………………………7分
![]()
![]()
![]() 的等比数列………………………………9分
的等比数列………………………………9分
![]() ………………………………………………………………………10分
………………………………………………………………………10分
(II)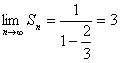 …………………………………………………………12分
…………………………………………………………12分
21.解:(I)200;………………………………………………………………………3分
(II)降低税率后的税率为(10-x)%,农产品的收购量为![]() 万吨,收购总金额为
万吨,收购总金额为![]()
故![]()
![]() ……………………………………………7分
……………………………………………7分
(III)原计划税收为![]() (万元),
(万元),
依题意得:![]()
解得![]()
![]() ………………………………………………………………………………11分
………………………………………………………………………………11分
答:x的取值范围是![]() …………………………………………………………12分
…………………………………………………………12分
22.解:(I)由函数![]() 单调递增,在区间
单调递增,在区间![]() 单调递减,
单调递减,
![]() ………………………………………………2分
………………………………………………2分
![]()
![]() ……………………………………………………………4分
……………………………………………………………4分
(II)点![]() ……6分
……6分
|
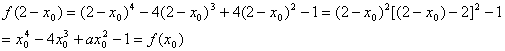
∴A关于直线x=1的对称点B也在函数f(x)的图象上………………………9分
(III)函数![]() 的图象与函数f(x)的图象恰有3个交点,等价于方程
的图象与函数f(x)的图象恰有3个交点,等价于方程
![]() 个不等实根…………………………………10分
个不等实根…………………………………10分
![]()
![]() 是其中一个根
是其中一个根
![]() 有两个非零不等实根…………………………12分
有两个非零不等实根…………………………12分
![]() ………………………………………14分
………………………………………14分