高三数列复习训练题
班级 学号 姓名 成绩
一、填空题
1. 在等差数列{an}中，
最大时，n的值是 .。
2.设{an}是公差为2的等差数列，
等于 .
3．在等比数列{an}中，已知
.
4．等差数列
的前n项和分别为
与
，若
，则
的值是 。
5．若四个正数a，b，c，d成等差数列，x是a和d的等差中项，y是b和c的等比中项，则x和y的大小关系是 .
6．．甲：数列{an}的前n项和Sn=an2+bn (a≠0)；乙: 数列{an}是等差数列；
则甲是乙的 条件
7．
是等差数列，S10>0，S11<0，则使
<0的最小的n值是 .
8．若一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，则这个数列的项数有 项 。
9．若
的前n项和是
.
10．在等差数列{an}中，已知公差d=5，前20项的和
.
11．已知数列
满足：
，则使
成立的n
的值是 ．
12．等差数列
的前n项和为Sn,且
如果存在正整数M，使得对一切正整数n，
都成立.则M的最小值是
.
二、选择题
13.已知数列的通项公式为
3n-50，则其前n项和Sn的最小值是 （ ）
A、-784 B、-392 C、-389 D、-368
14.等比数列中，Tn表示前n项的积，若T5=l，则
（ ）
A． al=l B．3a3=l C． a4=1 D．a5=l
15.等差数列{an}中，am+n=α，am-n=β，则其公差d的值为 （ ）
A．
B．
C．
D．
16．若
构成
（ ）
A．等差数列 B．等比数列
C．是等差数列也是等比数列 D．不是等差数列也不是等比数列
17．一张报纸，其厚度为a，面积为b，现将此报纸对折（既沿对边中点的连线折叠）
7次，这时报纸的厚度和面积分别是 （ ）
A．
B．
C．
D．
18．是实数构成的等比数列，Sn是其前n项和，则数列
中
（ ）
A．任一项均不为0 B．必有一项为0
C．至多有有限项为0 D．或无一项为0，或无穷多项为0
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
19．数列中，当n为奇数时，
，求这个数列的前2m项的和．
解：
20． 已知数列{an}的首项
是
以p为公比的等比数列. {an}的前n项和为
试问：S1，S2，S3……，Sn，……能否构成等差数列或等比数列，给出证明；
解：
21．已知数列满足
，对于任意的n∈N，都有＞0，且
.求数列的通项以及它的前n项和
.
解:
22. 数列{an}的前n项和为
（1）求通项an；
（2）是否存在常数a、b，使得对一切自然数n都有
成立.若存在，
求出a、b的值；若不存在，说明理由.
解：
23．已知等差数列{an}满足a1+a2n-1=2n(nÎN)，设Sn是数列{
}的前n项和，
记f(n)=S2n-Sn (nÎN)
(1)求an；
(2)比较f(n+1)与f(n)（其中nÎN）的大小;
(2) 如果函数g(x)=log2x-12f(n)（xÎ[a,b]）对一切大于1的自然数n其函数值都小于零，
那么a、b应满足什么条件？
解:
川沙中学2004届高三数列复习训练题解答
班级 学号 姓名 成绩
一、填空题
1. 在等差数列{an}中，最大时，n的值是 6，7 .。
2.设{an}是公差为2的等差数列，等于 82 .
3．在等比数列{an}中，已知 46 .
4．等差数列的前n项和分别为与，若，则的值是
。
5．若四个正数a，b，c，d成等差数列，x是a和d的等差中项，y是b和c的等比中项，则x和y的大小关系是 x≥y .
6．甲：数列{an}的前n项和Sn=an2+bn (a≠0)；乙: 数列{an}是等差数列；
则甲是乙的 充分非必要 条件.
7．是等差数列，S10>0，S11<0，则使<0的最小的n值是 6 .
8．若一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，则这个数列的项数有 13 项 。
9．若的前n项和是
.
10．在等差数列{an}中，已知公差d=5，前20项的和
2000 .
11．已知数列满足：，则使成立的n
的值是 21 ．
12．等差数列的前n项和为Sn,且如果存在正整数M，使得对一切正整数n，都成立.则M的最小值是 2 .
二、选择题
13.已知数列的通项公式为3n-50，则其前n项和Sn的最小值是 （ B ）
A、-784 B、-392 C、-389 D、-368
14.等比数列中，Tn表示前n项的积，若T5=l，则
（ B ）
A． al=l B．3a3=l C． a4=1 D．a5=l
15.等差数列{an}中，am+n=α，am-n=β，则其公差d的值为 （ B ）
A． B．
C． D．
16．若构成
（ A ）
A．等差数列 B．等比数列
C．是等差数列也是等比数列 D．不是等差数列也不是等比数列
17．一张报纸，其厚度为a，面积为b，现将此报纸对折（既沿对边中点的连线折叠）
7次，这时报纸的厚度和面积分别是 （ C ）
A． B． C． D．
18．是实数构成的等比数列，Sn是其前n项和，则数列中
（ D ）
A．任一项均不为0 B．必有一项为0
C．至多有有限项为0 D．或无一项为0，或无穷多项为0
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
19．数列中，当n为奇数时，，求这个数列的前2m项的和．
解：数列
是公差为10的等差数列，
是公比为2的等比数列，
．
20． 已知数列{an}的首项是
以p为公比的等比数列. {an}的前n项和为
试问：S1，S2，S3……，Sn，……能否构成等差数列或等比数列，给出证明；
解：
时an是以P为公比的等比数列，
P=1时 不合题意 ∴ p¹1
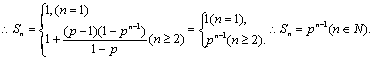
能构成等比数列，但不能构成等差数列.
21．已知数列满足，对于任意的n∈N，都有＞0，且
.求数列的通项以及它的前n项和.
解
＞0（ｎ∈N），且
，
∴ [(n+1)-n
](
)=0
∵ ＞0（ｎ∈N）， ∴ 
．
∴ 
．
又,所以，
．∴ 
．
22. 数列{an}的前n项和为
（1）求通项an；
（2）是否存在常数a、b，使得对一切自然数n都有成立.若存在，
求出a、b的值；若不存在，说明理由.
解：①
②假设存在这样的a,b，使得对一切自然数n都有
则
令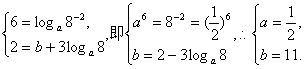
∴存在这样的数
23．已知等差数列{an}满足a1+a2n-1=2n(nÎN)，设Sn是数列{}的前n项和，
记f(n)=S2n-Sn (nÎN)
(1)求an；
(2)比较f(n+1)与f(n)（其中nÎN）的大小;
(3) 如果函数g(x)=log2x-12f(n)（xÎ[a,b]）对一切大于1的自然数n其函数值都小于零，
那么a、b应满足什么条件？
解: (1)设an=a1+(n-1)d (nÎN) 由 a1+a2n-1=2n
得 a1+a1+(2n-1-1)d=2n, 所以an= n, (3分)
(2)由 Sn=
得
f(n)=S2n-Sn=
=
(6分)
因为f(n+1)-f(n)= 
-
=
=
＞0 (9分)
所以f(n+1)＞f(n) (10分)
(3)由(2)可知, 数列{f(n)}的项的取值随n的增大而增大,
当n≥2时, f(n)的最小值为f(2)=
(12分)
所以问题转化为当xÎ[a,b]时, 函数g(x)=log2x的值恒小于7, (14分)
由函数y =log2x的性质可知, 在区间(0,27)上函数恒小于7, (16分)
所以, a、b应满足的条件是 0＜a＜b＜27.