高三数列复习训练题
一、填空题
1.已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列，则
＝ 。
2.．互不相等的三个实数x,y,z成等差数列，且x,z,y成等比数列，则x:y:z= 。
3． 已知数列
的通项公式
则
= 。
4．各项均为正数的等比数列{an}，若a5a6=9,则log3a1+log3a2+…+log3a10= 。
5．等差数列
和
的前n项和分别为Sn和Tn，对一切自然数n都有
，
则
等于 。
6已知等比数列的各项均为正数，公比
Q=
，则P与Q
的大小关系是 .
7. 已知等式1•22+2•32+…+n•(n+1)2=
n(n+1)(an2+bn+10)对一切自然数n 都成立，
那么a= ,b= .
8．在等差数列中，
则
=_
。
9．在等比数列中，已知
则
_________.
10．若
，数列的前n项和Sn=5，则n=_________。
11．
是等差数列，S10＞0，S11＜0，则使
＜0的最小的n值是
.
12．以下四个命题中
①{an}A.P.且p、q、rÎN，则“ap、aq、ar成等差数列”的充要条件是“p、q、r成等差数列”
②“
” 是“ a、b、c 成等比数列的必要不充分条件”；
③“{lgan}成A.P.”是“{an}成等比数列”的充分不必要条件；
④ m、n、p、rÎN，{an}是等比数列 ，“m+n=p+r”是“aman=apar”充要条件。
真命题个数为 。
二、选择题
13．．已知数列的首项
，又满足
则该数列的通项等于 （ ）
（A）
（B）
（C）
（D）
14．数列中，
，又数列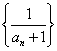
是等差数列，则
=
（ ）
（A）0
（B）
（C）
（D）－1
15．在等差数中，若
则
等于
（ ）
（A）90 （B）100 （C）110 （D）120
16．设是由正数组成的等比数列，公比
且
则
等于
（ ）
（A）
（B）
（C）
（D）
17．等差数列共有
项，其中
则的值为
（
）
（A）5 （B）3 （C）7 （D）9
18．已知
顺次成等差数列，则
（
）
（A）
有最大值，无最小值
（B）有最小值
，无最大值
（C）有最小值，最大值1 （D）有最小值 -1，最大值1
三、解答题
19.已知{an}是等差数列, 且an ≠ 0, (nÎN), 公差d ≠ 0. 设方程anx2+2an+1x+an+2= 0是关
于x的一组方程.
(1)求这组方程的公共根;
(2)证明: 如果上述方程的另一个根为bn , 则数列{
}是等差数列.
解：
20． (本小题满分14分)
在公差不为零的等差数列{an}和等比数列{bn}中，已知a1=１，且a1=b1，a2=b2，a6=b3
（Ⅰ）求公差和公比；
（Ⅱ）是否存在实数a,b，使得对于一切自然数n都有
+ｂ成立，若存在求出；
若不存在，说明理由.
解：
21．设An为数列{an}的前n项和，An=
(an-1）(nÎN)，数列{bn}的通项公式为bn=4n+3（nÎN)，（1）求数列{an}的通项公式；
（2）将数列{an}与{bn}的公共项按它们在原数列中的先后顺序排成一个新数列{cn}，求{cn}的通项公式；。
解：
22.(本小题满分14分)
在西部大开发中某公司投资兴办甲、乙两个企业，2000年甲企业获利润320万元，
乙企业获利润720万元，以后每年企业的利润甲以上年利润的1.5倍速度递增，而乙企
业是上年利润的
，预期目标为两企业年利润之和是1600万元，从2000年年初起
（Ⅰ）哪一年两企业获利润之和最小，最小值是多少?
（Ⅱ）经过几年即可达到预期的目标(精确到年).
解：
 |
23．
高三数列复习训练题解答
一、填空题
1.已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列，则＝
。
2.．互不相等的三个实数x,y,z成等差数列，且x,z,y成等比数列，则x:y:z= 4：1：(-2)。
3． 已知数列的通项公式则= 50 。
4．各项均为正数的等比数列{an}，若a5a6=9,则log3a1+log3a2+…+log3a10= 10 。
5．等差数列和的前n项和分别为Sn和Tn，对一切自然数n都有，
则 等于 
。
6已知等比数列的各项均为正数，公比Q=，则P与Q
的大小关系是 P>Q .
7. 已知等式1•22+2•32+…+n•(n+1)2=n(n+1)(an2+bn+10)对一切自然数n 都成立，
那么a= 3 ,b= 11 .
8．在等差数列中，则=__10_.
9．在等比数列中，已知则_____4____.
10．若，数列的前n项和Sn=5，则n=___35______。
11．是等差数列，S10＞0，S11＜0，则使＜0的最小的n值是 6 .
12．以下四个命题中
①{an}A.P.且p、q、rÎN，则“ap、aq、ar成等差数列”的充要条件是“p、q、r成等差数列”
②“ ” 是“ a、b、c 成等比数列的必要不充分条件”；
③“{lgan}成A.P.”是“{an}成等比数列”的充分不必要条件；
④ m、n、p、rÎN，{an}是等比数列 ，“m+n=p+r”是“aman=apar”充要条件。
真命题个数为 1 。选择题
二、选择题
13．．已知数列的首项，又满足则该数列的通项等于 （ B ）
（A） （B） （C） （D）
14．数列中，，又数列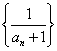是等差数列，则= （ B ）
（A）0
（B）
（C）
（D）-1
15．在等差数中，若则等于
（ B
）
（A）90 （B）100 （C）110 （D）120
16．设是由正数组成的等比数列，公比且
则等于
（ B ）
（A）
（B）
（C）
（D）
17．等差数列共有项，其中
则的值为
（ B ）
（A）5 （B）3 （C）7 （D）9
18．已知顺次成等差数列，则
（ B ）
（A）有最大值，无最小值
（B）有最小值，无最大值
（C）有最小值，最大值1 （D）有最小值 -1，最大值1
三、解答题
19.已知{an}是等差数列, 且an ≠ 0, (nÎN), 公差d ≠ 0. 设方程anx2+2an+1x+an+2= 0是关
于x的一组方程.
(1)求这组方程的公共根;
(2)证明: 如果上述方程的另一个根为bn , 则数列{}是等差数列.
解：（1）由已知2an+1=an+an+2 又由anx2+2an+1x+an+2= 0 Þ (x+1)(anx+an+2)=0
所以x= -1是这组方程的公共根; 方程的另一个根为bn=x= -
Þ -
得证
（2）由已知2an+1=an+an+2 又由anx2+2an+1x+an+2= 0 Þ (x+1)(anx+an+2)=0
所以x= -1是这组方程的公共根; 方程的另一个根为bn=x= -
Þ -得证.
20． (本小题满分14分)
在公差不为零的等差数列{an}和等比数列{bn}中，已知a1=１，且a1=b1，a2=b2，a6=b3
（Ⅰ）求公差和公比；
（Ⅱ）是否存在实数a,b，使得对于一切自然数n都有+ｂ成立，若存在求出；
若不存在，说明理由.
解：(Ⅰ)设公差为d(d≠0)，公比为q 1分
由条件：b1=1,且a2=b2,a6=b3
∴
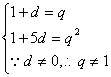解得d=3
q=4
6分
(Ⅱ)若存在a、b对一切自然数n都有an=logabn+b
即由(1)得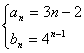
8分
∴3n-2=loga4n-1+b ∴(3-loga4)n+(loga4-b-2)=0恒成立
∴
12分
∴ 
14分
21．设An为数列{an}的前n项和，An=(an-1）(nÎN)，数列{bn}的通项公式为bn=4n+3（nÎN)，（1）求数列{an}的通项公式；
（2）将数列{an}与{bn}的公共项按它们在原数列中的先后顺序排成一个新数列{cn}，求{cn}的通项公式；。
解：（1）An=(an-1)，Þ An+1=(an+1-1)，相减 Þ An+1-An=an+1-an，Þan+1=an+1-an，Þ an+1=3an(nÎN)
a1=(a1-1) Þ a1=3，Þ 数列{an}是以3为首项，3为公比的等到比数刑，Þ an=3n
。
（2）a1=3，a2=9，{bn}的项，a3=27=4´6+3=b6，∴ c1=a3=b6=27，设cn=am=bp，Þ 3m=4p+3，数列an+1=3m+1=3×3m=3(4p+3)=4(3p+2)+1，∴am+1不是{bn}的项，
又an+2=3m+2=9×3m=9(4p+3)=9(9p+6)+3，∴am+1是{bn}的项，∴
=9，ÞCn=c1×qn-1=27×9n-1=32n+1，故{cn}的通项公式为Cn=32n+1
。
22.(本小题满分14分)
在西部大开发中某公司投资兴办甲、乙两个企业，2000年甲企业获利润320万元，
乙企业获利润720万元，以后每年企业的利润甲以上年利润的1.5倍速度递增，而乙企
业是上年利润的，预期目标为两企业年利润之和是1600万元，从2000年年初起
（Ⅰ）哪一年两企业获利润之和最小，最小值是多少?
（Ⅱ）经过几年即可达到预期的目标(精确到年).
解：(Ⅰ)设从2000年起，第n年获利润为yn
由条件：
3分
≥
=2×480=960 5分
当且仅当
6分
即
∴n=2时取“=”.故第二年即2001年上交利润最少，共960万元---7分
(Ⅱ)由题意：
≥1600化简为：
9分设
，原不等式化为4t2-20t+9≥0解得：t≥
或t≤
(舍) 1 2分
由t≥得
≥ ∴n≥
13分
∴n=5，即经过5年可达到预期目标 14分
|
23．