高三数学测试题
数学试题(文科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.准线方程为![]() 的抛物线的标准方程为 ( )
的抛物线的标准方程为 ( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
2.函数![]() 是 ( )
是 ( )
(A) 最小正周期为π的奇函数 (B) 最小正周期为π的偶函数
(C) 最小正周期为2π的奇函数 (D) 最小正周期为2π的偶函数
3.函数![]() 的反函数是 ( )
的反函数是 ( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
4.已知向量![]() 平行,则x等于 ( )
平行,则x等于 ( )
(A)-6 (B) 6 (C)-4 (D) 4
5.![]() 是直线
是直线![]() 垂直的 ( )
垂直的 ( )
(A).充分而不必要的条件 (B).必要而不充分的条件
(C).充要条件 (D).既不充分又不必要的条件
6.已知直线a、b与平面α,给出下列四个命题
①若a∥b,b![]() α,则a∥α; ②若a∥α,b
α,则a∥α; ②若a∥α,b![]() α,则a∥b ;
α,则a∥b ;
③若a∥α,b∥α,则a∥b; ④a⊥α,b∥α,则a⊥b.
其中正确的命题是 ( )
(A).1个 (B).2个 (C).3个 (D).4个
7.函数![]() 的单调递增区间是 ( )
的单调递增区间是 ( )
(A).![]() (B).
(B).![]()
(C).![]() (D).
(D).![]()
8.设集合M=![]() 是 ( )
是 ( )
(A).![]() (B).有限集 (C).M (D).N
(B).有限集 (C).M (D).N
9.已知函数![]() 的最小值是 ( )
的最小值是 ( )
(A) ![]() (B).2 (C).
(B).2 (C).![]() (D).
(D). ![]()
10.若双曲线![]() 的左支上一点P(a,b)到直线
的左支上一点P(a,b)到直线![]() 的距离为
的距离为![]() +b的值为 ( )
+b的值为 ( )
(A).![]() (B).
(B).![]() (C).-2 (D).2
(C).-2 (D).2
11.若一个四面体由长度为1,2,3的三种棱所构成,则这样的四面体的个数是 ( )
(A).2 (B).4 (C).6 (D).8
12.某债券市场常年发行三种债券,A种面值为1000元,一年到期本息和为1040元;B种贴水债券面值为1000元,但买入价为960元,一年到期本息和为1000元;C种面值为1000元,半年到期本息和为1020元. 设这三种债券的年收益率分别为a, b, c,则a, b, c的大小关系是 ( )
(A).![]() ( B).
( B).![]() (C).
(C).![]() (D).
(D).![]()
第Ⅱ卷(非选择题共90分)
二、填空题:(本大题共4小题,每小题4分,共16分,把答案直接填在题中横线上.)
13.某校有初中学生1200人,高中学生900人,老师120人,现用分层抽样方法从所有师生中抽取一个容量为N的样本进行调查,如果应从高中学生中抽取60人,那么N
.
14.在经济学中,定义![]() 的边际函数,某企业的一种产品的利润函数
的边际函数,某企业的一种产品的利润函数![]() *),则它的边际函数MP(x)=
.(注:用多项式表示)
*),则它的边际函数MP(x)=
.(注:用多项式表示)
15.已知![]() 分别为△ABC的三边,且
分别为△ABC的三边,且![]() .
.
16.已知下列四个函数:①![]() ②
②![]() ③
③![]() ④
④![]() .其中图象不经过第一象限的函数有
.(注:把你认为符合条件的函数的序号都填上)
.其中图象不经过第一象限的函数有
.(注:把你认为符合条件的函数的序号都填上)
三、解答题:(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
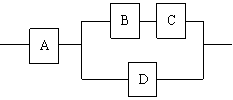 如图:用A、B、C、D四类不同的元件连接成系统N,当元件A正常工作且元件B、C都正常工作,或当元件A正常工作且元件D正常工作时,系统N正常工作.已知元件A、B、C、D正常工作的概率依次为
如图:用A、B、C、D四类不同的元件连接成系统N,当元件A正常工作且元件B、C都正常工作,或当元件A正常工作且元件D正常工作时,系统N正常工作.已知元件A、B、C、D正常工作的概率依次为![]()
(Ⅰ)求元件A不正常工作的概率;
(Ⅱ)求元件A、B、C都正常工作的概率;
(Ⅲ)求系统N正常工作的概率.
18.(本小题满分12分)
已知函数![]() 的图象过点
的图象过点![]()
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)记![]() 是正整数,Sn是数列{an}的前n项的和,求S30.
是正整数,Sn是数列{an}的前n项的和,求S30.
19.(本小题满分12分)
把长240cm,宽90cm的矩形铁皮的四角切去相等的正方形,然后折成一个无盖的长方
体的盒子,角上切去的正方形的边长为多少时,盒子的容积最大. 最大容积是多少?
20.(本小题满分12分)
如图:已知四棱锥P—ABCD的底面为直角梯形,AD∥BC,∠BCD=90,PA=PB,PC=PD.
(Ⅰ)证明CD与平面PAD不垂直;
(Ⅱ)证明平面PAB⊥平面ABCD;
(Ⅲ)如果CD=AD+BC,二面角P—BC—A等于60°,求二面角P—CD—A的大小.
 |
21.(本小题满分12分)
已知椭圆的中心在原点,焦点在y轴上,焦距为4,离心率为![]()
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆在y轴的正半轴上的焦点为M,又点A和B在椭圆上,且M分有向线段![]() 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.
22.(本小题满分14分)
设函数![]()
(Ⅰ)解不等式![]()
(Ⅱ)求a的取值范围,使f(x)在区间(0,+∞)上是单调减函数.
天 津 大 港 高 三 质 量 调 查
数学试题(文科)参考答案及评分标准
一、选择题:(每小题5分,共60分)
BADCA ABDCA BC
二、填空题:(每小题4分,共16分)
13.148; 14.![]() 且
且![]() (未标定义域扣1分);
(未标定义域扣1分);
15.![]() ; 16.①,④(多填少填均不给分)
; 16.①,④(多填少填均不给分)
三、解答题:(共74分,以下为累计得分,其它解法请相应给分)
17.解:(Ⅰ)元件A正常工作的概率![]() ,
,
它不正常工作的概率![]() (2分)
(2分)![]() ;(3分)
;(3分)
(Ⅱ)元件A、B、C都正常工作的概率![]() (5分)
(5分)
![]() ;(6分)
;(6分)
(Ⅲ)系统N正常工作可分为A、B、C都正常工作和A、D正常但B、C不都正常工作两种情况,前者概率![]() ,(7分)后者的概率为
,(7分)后者的概率为![]() (10分)
(10分)
![]() (11分),所以系统N正常工作的概率是
(11分),所以系统N正常工作的概率是![]() (12分)
(12分)
18.解:(Ⅰ)由题意得![]() (2分) 解得
(2分) 解得![]() (4分)
(4分) ![]() (5分)
(5分)
(Ⅱ)![]() (6分)
(6分)![]() (7分)
(7分)
因为![]() 故
故![]() 是等差数列.(8分) 且
是等差数列.(8分) 且![]() ,(9分)
,(9分)
由![]() ,(10分) 得
,(10分) 得![]() .(12分)
.(12分)
19.解:设切去的正方形的边长为![]() cm,则折成的无盖的长方体 底面边长为
cm,则折成的无盖的长方体 底面边长为![]() cm和
cm和![]() cm(2分),高为
cm(2分),高为![]() cm,于是盒子的容积(单位:
cm,于是盒子的容积(单位:![]() )
)
![]() (4分)
(4分)
又由![]() ,得
,得![]() .
. ![]() .(6 分)
.(6 分)
令![]() ,得
,得![]() ,由
,由![]() ,解得
,解得![]() .(8分) 当
.(8分) 当![]() 时,
时,![]() 时,
时,![]() ,因此当
,因此当![]() 时,V有最大值(10分) 最大容积
时,V有最大值(10分) 最大容积![]() (12分)
(12分)
20.解:(Ⅰ)若CD⊥平面PAD(1分),则CD⊥PD(2分),由已知PC=PD,得
∠PCD=∠PDC![]() , 这与CD⊥PD矛盾,所以CD与平面PAD不垂直.(3分)
, 这与CD⊥PD矛盾,所以CD与平面PAD不垂直.(3分)
(Ⅱ)取AB、CD的中点E、F,连接PE、PF、EF(4分),由PA=PB,PC=PD,得PE⊥AB,
PF⊥CD(5分)∴EF为直角梯形的中位线,∴EF⊥CD,又PF∩EF=F,∴CD⊥平面PEF,(6分)由PE![]() 平面PEF,得CD⊥PE,又AB⊥PE且梯形两腰AB、CD必交,∴PE⊥平面ABCD(7分)又PE
平面PEF,得CD⊥PE,又AB⊥PE且梯形两腰AB、CD必交,∴PE⊥平面ABCD(7分)又PE![]() 平面PAB,∴平面PAB⊥平面ABCD(8分)
平面PAB,∴平面PAB⊥平面ABCD(8分)
(Ⅲ)由(Ⅱ)及二面角的定义知∠PFE为二面角P-CD-A的平面角(9分)作EG⊥BC于G,连PG,由三垂线定理得BC⊥PG,故∠PGE为二面角P-BC-A的平面角(10分)
即∠PGE=60°,由已知,得![]() ,又EG=CF=
,又EG=CF=![]() CD.∴EF=EG,易证得Rt⊿PEF≌Rt⊿PEG.(11分)∴∠PEF=∠PGE=60°,即为所求.(12分)
CD.∴EF=EG,易证得Rt⊿PEF≌Rt⊿PEG.(11分)∴∠PEF=∠PGE=60°,即为所求.(12分)
21.解:(Ⅰ)设椭圆方程为![]() (1分) 由2c=4得c=2,又
(1分) 由2c=4得c=2,又![]() ,故
,故![]() (2分)
(2分)
![]() ,∴所求椭圆方程为
,∴所求椭圆方程为![]() (3分)
(3分)
(Ⅱ)M坐标为(0,2),设A点在B点的左方,且![]() ,由
,由![]() ,故有
,故有
![]() (5分)即
(5分)即![]() ①,又M相应的准线方程是
①,又M相应的准线方程是![]() ,A到准线距离
,A到准线距离
![]() ,B到准线距离
,B到准线距离![]() (6分),由
(6分),由![]() 及
及![]() (7分)
(7分)
于是![]() ,∴
,∴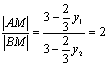 得
得![]() ②
②
②与①联立解得![]() (8分) 代入椭圆方程得
(8分) 代入椭圆方程得![]() ,∴直线AB的斜率
,∴直线AB的斜率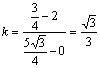 (9分),AB的方程为
(9分),AB的方程为![]() (10分),如果点在B的右方时根据对称性,则所求直线AB的方程为
(10分),如果点在B的右方时根据对称性,则所求直线AB的方程为![]() .(12分)
.(12分)
22.(Ⅰ)由![]() ,化为
,化为![]() (1分)⑴当
(1分)⑴当![]() 时,不等式化为
时,不等式化为![]() 解集为
解集为![]() ,(3分)⑵当
,(3分)⑵当![]() 时,有
时,有![]() 解集为
解集为![]() (5分)⑶当
(5分)⑶当![]() 时,化为
时,化为![]() 解集为
解集为![]() (8分)⑷当
(8分)⑷当![]() 时,有
时,有![]() ,解集为
,解集为![]() .(10分)
.(10分)
(Ⅱ)在区间![]() 上任取
上任取![]() ,则
,则![]() (11分)
(11分)![]() (12分) 因
(12分) 因![]() 故
故![]() ,又在
,又在![]() 上
上![]() ,
,![]()
∴只有当![]() 时,即
时,即![]() 时。才总有
时。才总有![]() ,∴当
,∴当![]() 时,
时,![]() 在
在![]() 上是单调减函数.(14分)
上是单调减函数.(14分)