高三数学单元测试（1、2章）
一、选择题：
1、设全集
为自然数列
，
，
，那么集合可
以表示成····································································································· （ ）
（A）
； （B）
； （C）
； （D）
.
2、函数
，它们的定义域都是
，则函数
的定义域是····································································· （ ）
（A）
； （B）
； （C）
； （D）
.
3、已知函数
的图象经过点
，又其反函数
的图象经过点
,
则函数
的表达式是················································································ （ ）
（A）
；
（B）
；
（C）
；
（D）
.
4、已知
，则
是
的（ ）
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、非充分也非必要条件
5、若是奇函数，且
时，
，则当
时，的解析式是 （ ）
（A）
（B）
（C）
（D）
.
6、 若函数
在区间（-1，0）上有
，则的递增区间是
7、已知函数的图象与函数
的图象关于直线
对称，则
的单调递减区间为····················································································· （ ）
（A）
； （B）
； （C）
； （D）∪.
8、设
为偶函数，
为奇函数那么
的值为（ ）
A、1 B、
C、
D、
9、若
，则下列各式中正确的是 ·························································· （ ）
（A）
；
（B）
；
（C）
；
（D）
.
10、已知
，且关于
的方程
有实根，则
等于 （ ）
（A）0； （B）1； （C）2； （D）3.
11、设是定义在
上的偶函数,且在
上为减函数,
，
，则
的大小关系为···················································· （ ）
（A）
； （B）
； （C）
； （D）
.
12、设
的两根是α、β，则
的最小值是 （ ）
（A）2 （B）－2 （C）1 （D）3
二、填空题：
13、已知函数
，则的定义域是
.
14、函数
的值域是
.
15、函数
的反函数是
.
16、设集合A={│
}，B={│
，若
的取值范围是_____________________________。
三、解答题：
17、(12分)解方程：
.
18、（１2分）设
是定义在
上的函数，且满足关系
．
(Ⅰ)求的解析式；
(Ⅱ)当取何值时，有最大值和最小值？最大值和最小值各是多少？
19、（本小题满分１4分）设a∈R，f(x)为奇函数，f(2x)=
（1）求f(x)的反函数f-1(x)及其定义域；
（2）设g(x)=
，若x∈[,
]，f-1(x) ≤g(x)恒成立，求实数k的取值范围。
20、（12分）设为实数，函数
，
（1）讨论的奇偶性；
（2）求的最小值。
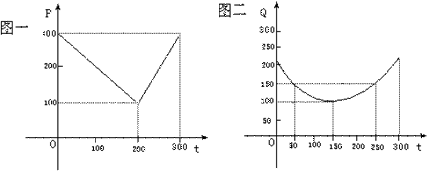21、某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场售价与上市时间的关系用图一的一条折线表示；西红柿的种植成本与上市时间的关系用图二的抛物线段表示.(2000(21)12分)
⑴写出图一表示的市场售价与时间的函数关系P＝f(t)；
写出图二表示的种植成本与时间的函数关系式Q＝g(t)；
⑵认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？
(注：市场售价和种植成本的单位：元/10kg，时间单位：天)
22、（本小题满分14分）已知二次函数
满足条件：
=
，且方程
=
有等根。
(Ⅰ)求的解析式；
(Ⅱ)是否存在实数m、n (m<n)，使的定义域和值域分别是[m，n]和[3m，3n]?如果存在，求出m、n的值；若不存在，说明理由。
参考答案：
选择题：CDAAB CCDAB BA 填空题：13、
14、
15、
16、
解答题：17、原方程的解为：
18、（1）
（2）
；
19、（1）
（2）
20、（1）
，为偶函数；
，非奇函数非偶函数 （2）
；
；
21、
，
（2）第50天时，最大收益为100 22、（1）
（2）存在
。