高三数学普通高中毕业考试

秘密★启用前

高三数学普通高中毕业考试

数　 学

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至3页，第Ⅱ卷4至7页．共100分．考试时间100分钟．

第　I　卷 （选择题　共60分）

注意事项：

1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.

　　2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上.

3．考试结束，监考人员将本试卷和答题卡一并交回.

　　参考公式：

三角函数的积化和差公式　　　　　　　正棱台、圆台的侧面积公式：

　　　 　 其中、分别表上、　　　 下底面周长，表示斜高或母线长

　　  台体的体积公式：

　　  其中、S分别表示上、下底面积，h表示高

一．选择题：本大题共20小题，每小题3分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

（1）已知集合A={x－2≤x≤2}，集合B={x0＜x＜3}，则A∪B=

（A）{x－2≤x≤3}　　　　　　　　　　　（B）{x－2≤x＜3}　　　　 

（C）{x0≤x＜2}　　　　 　　　　　　　 （D）{x0＜x≤2}

（2）函数y=2sin（2x ＋）的最小正周期是

　　（A）　　　　　 （B）π　　　　　  （C）2π　　　　　   （D）4π

（3）直线x＋3y－2=0的斜率是

　　（A）－　 　　 （B） 　　　　 （C）－　　　  （D）

（4） 已知函数f(x)=x²(x≥0)，则f ^－1()的值为　　　　　　　　　

　　 （A）　　　 　（B）　　　　 　 （C）—　　 　　（D）—

（5） 等于

　　 （A）2　　　　　　（B）－2　　　　   （C）－　　　　 （D）

（6） 椭圆的焦点坐标为

　　 （A）（0，5）和（0，—5）　　　　　　  （B）（5，0）和（—5，0）

　　 （C）（0，）和（0，—）　　　　 （D）（，0）和（—，0）

（7）sin20°sin10°—cos20°cos10°的值为

　　 （A）—　　  （B）—　　　　　 （C）　　　 　　（D）

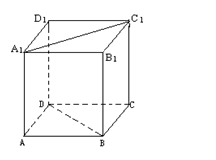
（8） 正四棱柱ABCD—A₁B₁C₁D₁中，

A₁C₁与BD所在直线所成角的大小是

　　 （A）30° 

　　 （B）45° 

　　 （C）60°

  （D）90°

（9） 函数y=log₂（2x－1）的定义域为

 （A）{xx＞0}　　　　　　　　 　　　 （B）{xx＞}　　　　　　　   

 （C）{xx＜}　　　　　　　  　　　 （D）{xx≥}

（10）不等式≤1的解集是

 （A）{xx≤2}　　　　　　　  　　　　 （B）{x1＜x≤2}　　　

 （C）{x1≤x≤2}　　　 　　　　　　　 （D）{x1≤x＜2}

（11） 双曲线的渐近线方程为

 （A）x±2y=0　　　　　　　　  　　　 （B）2x±y=0　　　　　　　　　 

 （C）x±y=0　　　　　　　　　 　　（D）x±y=0

（12） 已知cos=，则cosα的值为

　　 （A）－　　　　 （B）　　　 　　（C）－　　　　  （D）

（13） 已知一个球的面积为16π，则这个球的体积为

　　　（A）π　　　　（B）π　　　　（C）π　　　 　（D）π

（14） 如果数列{a_n}中，a₁=1，a_n=a_n-1（n＞1，n∈N），则a₁＋a₂＋a₃＋a₄＋a₅＋a₆=

　　  （A）63　　　　  （B）　　　 　 （C） 　　　　 （D）

（15） 已知0＜a＜1，则下列各式中，其值最大的是

　　　（A）a^-2　　　　　　　 （B）a²　　　　（C） log _a 1　　 　（D） log _a3

（16）复数z= －1＋i 的三角形式是

　　　（A）2（cos＋isin）　　　　　  （B）2（cos＋isin）

　　　（C）2（cos＋isin）　　　　　  （D）2（cos＋isin）

（17）要得到函数y=2cos（2x－）的图象，只需将函数y=2cos2x的图象

　　　（A）向左平移个单位　　　　　　　 （B） 向右平移个单位

　　　（C） 向左平移个单位　　　　　　  （D） 向右平移个单位

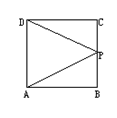
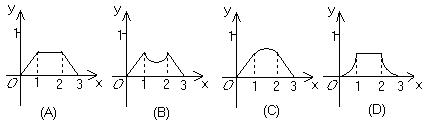
（18）如图，动点P在边长为1的正方形ABCD的边上沿ABCD运动，x表示动点P由A点出发所经过的路程，y表示△APD的面积，则函数y=f（x）的图象的草图是

（19） 下列四个命题中，正确的命题是

　　　（A）两条直线与一个平面所成的角相等，则这两条直线平行
　　　（B）两个平面平行，其中一个平面内的直线必平行于另一个平面
　　　（C）一个平面内无数条直线与另一个平面平行，则这两个平面平行
　　　（D）过平面外一点作与这个平面垂直的平面有且只有一个

（20）某商品零售价2002年比2001年上涨25%，欲使2003年比2001年上涨10%，则2003年比2002年应降价

 （A）12%　　　　（B）15%　　　　 （C）5%　　　　 （D）10%

 秘密★启用前

普通高中毕业考试

数　 学

第　Ⅱ　卷（非选择题　共40分）

注意事项：

1．　第Ⅱ卷共4页，用蓝、黑墨水钢笔或圆珠笔直接答在试题卷中.

2．　答卷前将密封线内的项目填写清楚，并在试卷右上角填上座位号.

题号	二	三				总分
		25	26	27	28
分数

二．填空题：本大题共4小题，每小题3分，共12分．把答案填在题中横线上．   得分	评卷人

(21) 已知一个圆柱的轴截面是边长为2的正方形，则这个圆柱的侧面积为　　　　　　　 .

(22) (x －)⁶展开式中x²的系数为　　　　　  .（用数值作答）

(23) 抛物线y = 4x² 的准线方程为　　　　　　　　  .

(24) 某校一个数学研究性学习小组共有8个同学，其中男同学5人，女同学3人.现从这8个同学中选出3人准备一个报告会，要求在选出的3人中男、女同学都有，则不同的选法共有　　　　　　  种（用数字作答）.

三．解答题：本大题共4小题，共28分．解答应写出文字说明．证明过程或演算步骤．

(25)（本小题满分6分）   得分	评卷人

　　　已知一个圆的圆心坐标为C（－1，2），且过点P（2，－2），求这个圆的标准方程.

(26)（本小题满分6分）   得分	评卷人

　　　在1和15之间插入两个正数，使前三个数成等比数列，后三个数成等差数列，求这两个正数.

(27)（本小题满分7分）   得分	评卷人

　　　如图，已知CD是等边三角形ABC边AB上的高，沿CD将△ADC折起，使平面ADC与平面BDC互相垂直（如图2）.在图2中

　 （Ⅰ）求AB与平面BDC所成的角；

　 （Ⅱ）若O点在DC上，且分DC的比为，求二面角A-BO-C的正切值.

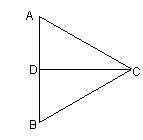
　　　　　　　　　　　　　　　　 图1　　　　　　　　　　　　 图2

 

(28)（本小题满分9分）   得分	评卷人

　　 已知函数f（x）=3ax²＋(a—2)x +a满足f（－1）≥a²+4，

　 （Ⅰ）求a的取值范围；

　 （Ⅱ）求证：3≤f（）≤.

广州市普通高中毕业考试

数学试题参考答案

一、选择题：本大题共20小题，每小题3分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

　　 （1）B　 （2）B 　 （3）A　　 （4）A　　（5）A　 （6）D　　（7）A　　

　　 （8）D　 （9）B　  （10）C　 （11）D　 （12）A  （13）B　 （14）D　

　　（15）A　（16）C　　（17）D　 （18）A　 （19）B　（20）A.

二、填空题：本大题共4小题，每小题3分，共12分，把答案填在题中横线上.

（21）4π；　　 （22）15；　　 （23）y= －；　　 （24）45.

三、解答题：本大题共4小题，共28分．解答应写出文字说明．证明过程或演算步骤．题

（25）解：依题意可设所求圆的方程为

(x＋1)²+(y－2)²= r ²--------------------------------------------2分

因为点P（2，－2）在圆上，所以

r² =(2＋1)²+(－2－2)²=25-------------------------------------4分

因此，所求的圆的标准方程是

(x＋1)²+(y－2)²=5 ²--------------------------------------------6分

（26）解：设插入的两个正数为a，b，依题意，得

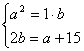---------------------------------------------------------2分

消去b，得

2a²－a－15=0---------------------------------------------------------3分

解之得

a=3或a= －（舍去）------------------------------------------4分

当a=3时，b=9.------------------------------- ------------------------------------------5分

故所插入的两个正数为3和9-----------------.-----------------------------------------6分

（27）（Ⅰ）解：∵　A-DC-B为直二面角，且AD⊥DC.

∴　AD⊥平面BDC

∴　AB与平面BDC所成的角为∠ABD------------------------------------------2分

∵　AD=BD，∠ADB=90°

∴　∠ABD=45°

∴　AB与平面BDC所成的角为45°.--------------------------------------------3分

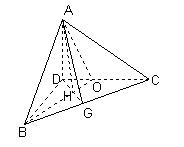
（Ⅱ）解：如图，过D作BO的垂线交BO于H，并延长交BC于G，连AH，AG

∵　 AD⊥平面BDC，又DH⊥BO

∴　 BO⊥AH（三垂线定理）

∴　 ∠AHG为二面角A-BO-G的平面角-----------------------------------------5分

∵　点O在DC上，且，则DO=OC=BO

∴　 ∠DBO=30°

∴　 BD=2DH

即　 AD=2DH　　　　

　　在Rt△ADH中，tg∠AHD=2----------------------------------------6分

∴　 tg∠AHG=tg（π－∠AHD）= －2

故二面角A-BO-C的正切值为－2.--------------------------------------------------7分

（28）（Ⅰ）解：∵　f（x）=3a x²＋(a—2)x+a

　　　　　　　 ∴　由f（－1）≥a²+4，得

3a(－1)²+(a—2)(－1)+a≥a²+4---------------------------------------1分

即　　　　 a²—3a+2≤0

即　　　　 （a—1）（a—2）≤0----------------------------------------------------2分

解之得　　 1≤a≤2------------------ --------------------------------------------------3分

∴　所求a的取值范围为{a1≤a≤2}.-----------------------------------------------4分

（Ⅱ）证明：∵　f（x）= 3a x²＋(a—2)x+a

  　　　　　　　∴　f ()=3a·＋(a—2) ·+a

即　　　　　　　　  f ()=+a+1-----------------------------------------------5分

令　t=

则由1≤a≤2得，≤t≤1------------------------------------------------------------6分

下面证明f (t)=t++1在[，1]上是减函数.

设≤t₁＜t₂≤1，则

f (t₁)—f (t₂)=t₁++1—（t₂++1）

　　　　  =

∵≤t₁＜t₂≤1

∴t₁—t₂＜0， 0＜t₁t₂＜1

∴ f (t₁)—f (t₂)＞0　

∴f (t)=t++1在[，1]上是减函数.-------------------------------------------8分

∴3≤f（t）≤.

即 3≤f（）≤.---------------------------------------------------------------9分