高三数学试题
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，共150分，考试时间120分钟。
第Ⅰ卷（选择题 共60分）
一、选择题：（本大题共12小题，共60分.）
1、若使集合M={xax2+2x+a=0,a
}中有且仅有一个元素a的所有的值组成集合N，则[ ]
A、N={-1,1} B、N={0,1}
C、N
{0,-1,1} D、N{-2,-1,0,1,2}
2、若复数z满足z2+z+1=0，则复数z+(z+1)4的值为[ ]
A、1
B、-1
C、 
D、
i
3、设A是原命题，
是A的否命题.若B是的必要非充分条件，那么A是
的[ ]
A、充分非必要条件 B、必要非充分条件 C、充要条件 D、非充分非必要条件
4、设函数f(x)=2x,(x
)的反函数y=
,则y=
的定义域为[ ]
A、 
B、 
C、 
D、
5、已知
是离散随机变量， 
那么[ ]
A、
B、
C、
D、
6、定义在R上的偶函数y=f(x)满足f(x+1)=-f(x)且在区间[-1,0]上是增函数,设a=f(
),b=f(2)，c=f(3)则[ ]
A、c<a<b B、b<c<a C、c< b< a D、 a<b<c
7、一个容量为20的样本数据分组后，组距与频数如下：
，2；
，3；
，4；
，5；
，4；
，2；则样本在
上的频率为[ ]
A、
B、
C、
D、 
8、无穷等比数列{an}的前n项和为Sn.若a1a2a3=8.且3(a2+a4+……+a2n)= S2n.则
[ ]
A、1 B、4 C、8 D、16
9、等差数列{an}中,a1= -5,它的前11项的平均值是5，若从中抽出一项，余下10项的平均值
是4，则抽取的一项是[ ]
A、a8 B、a9 C、a10 D、a11
10、 给出下列命题：
（1） 若函数f(x)=x，则f’(0)=0；
（2） 若函数f(x)=2x2+1，图象上P(1,3)及邻近上点Q(1+Δx,3+Δy)，
则
=4+2Δx
（3） 加速度是动点位移函数S(t)对时间t的导数；
（4）
y=2cosx+lgx，则y’=-2cosx·sinx+
其中正确的命题有[ ]
A、0个 B、1个 C、2个 D、3个
11、函数
的图象与函数
的图象在区间
上的交点情况是[ ]
A、至少有一个交点 B、至多有一个交点
C、至少有两个交点 D、至多有两个交点
12、某债券市场常年发行三种债券，A种面值为1000元，一年到期本息和为1040元；B种贴水债券面值为1000元，但买入价为960元，一年到期本息和为1000元；C种面值为1000元，半年到期本息和为1020元. 设这三种债券的年收益率分别为a, b, c，则a, b, c的大小关系是 [ ]
A、
B、
C、
D、
第Ⅱ卷（非选择题共90分）
二、填空题（本大题共4小题，共16分.）
13、函数y=tan2x-cot2x的最小正周期是_________
14、若
,则
在
方向上的投影为____________
15、对于任意实数x、y，定义运算x
y=(x+1)(y+1)-1，则以下四个结论成立的命题有_____
(1)
对于任意实数x、y, xy= yx
(2)
对于任意实数x、y、z, x
(y+1)=( xy)+( xz)
(3)
对于任意实数x、y、z, x(yz)= ( xy) z
(4)
对于任意实数x、y, x0=x
16、已知函数f(x)满足对任意x1<x2有f(x1)<f(x2),且f(x1+x2)=f(x1)f(x2)，写出一个满足这些条件的函数（只需写出一个即可）______
三、解答题：(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）
17、（本小题满分12分）
已知
有极大值
和极小值
.
(1)求+的值；
(2)设曲线y=f(x)的极值点为A、B，求证：线段AB的中点在y=f(x)上.
18、（本小题满分12分）
已知函数f（x）=3x+k（k为常熟）,A(-2k,2)是函数y=图像上一点
（Ⅰ）求实数k的值及函数y=的解析式
（Ⅱ）将y=的图像沿x轴向右平移3个单位得到的y=g(x)图像，求函数
F(x)=2-g(x)的最小值.
19、（本小题满分12分）
设一部机器在一天内发生故障的概率为0.2，机器发生故障时全天停止工作.若一周5个工作日里均无故障，可获利润10万元；发生一次故障可获利润5万元，只发生两次故障可获利润0万元，发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少？
20、（本小题满分12分）
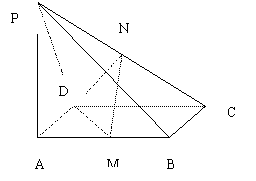
如图，PA⊥矩形ABCD所在平面，PA=AD=a，M，N分别是AB，PC的中点。
(I)求证：平面MND⊥平面PCD:
(II) 若AB=
,求二面角N-MD-C的大小
21、（本小题满分14分）
某村2002年底全村共有1000人，全年工农业总产值为840万元．
（I）若从2003年起该村每年的工农业总产值较上年增加14 万元，每年人口较上年净增数相同，要使该村人均产值年年都增长，那么该村每年人口的净增不超过多少人？
（II）若从2003年起该村每年工农业总产值较上年增长
，每年人口较上年净增10人，则到2012年该村能否实现年人均产值较2002年翻一番（增加一倍）的经济发展目标？
22、（本小题满分14分）
已知动点
与双曲线
的两个焦点
、
的距离之和为定值，且
的最小值为
．
（I）求动点的轨迹方程；
（II）若已知
，
、
在动点的轨迹上且
，求实数
的取值范围．