高三数学试题答案
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，共150分，考试时间120分钟。
第Ⅰ卷（选择题 共60分）
一、选择题：（本大题共12小题，共60分.）
1-6、 DBBDAA 7-12、DDDBBC
第Ⅱ卷（非选择题共90分）
二、填空题（本大题共4小题，共16分.）
13、
14、
15、（1）（3）（4）
16、f(x)=
（只需写出一个即可）
三、解答题：(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤)
17、解(1)f’(x)=3x2+2ax+b=0两根为
、
∴
，
…………………………………. (3分)
… (6分)
(2)A(,f())，B(,f())，其中点M(
)
∵
∴M在y=f(x)图象上 …………………… (12分)
18、解：(I)由题意 k=-3
y=
……………………
(6分)
(II) 
F(x)= 
=……
当x=3时F(x)=2
-g(x)的最小值是
………………
(12分)
19、解：以X表示一周5天内机器发生故障的天数，则X－B(5，0.2)，于是X有概率分布P(X=k)=C
0.2k0.85－k,k=0,1,2,3,4,5.
以Y表示一周内所获利润，则
Y=g(X)=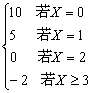
Y的概率分布为： …… (3分)
P(Y=10)=P(X=0)=0.85=0.328
P(Y=5)=P(X=1)=C
0.2·0.84=0.410
P(Y=0)=P(X=2)=C
·0.22·0.83=0.205
P(Y=－2)=P(X≥3)=1－P(X=0)－P(X=1)－P(X=2)=0.057……(8分)
故一周内的期望利润为：
EY=10×0.328+5×0.410+0×0.205－2×0.057=5.216(万元) ……(12分)
20、解：（1）∵M、N分别是AB、PC的中点，可得
,
由于
,
及
,
∴MN⊥CD,又MN⊥DP, ∴MN⊥平面PCD, ∴平面MND⊥平面PCD. ……(6分)
（2）底面的法向量为
，设平面MN的法向量为
,
,∴
.
,∴
.
∴
,
∴
,
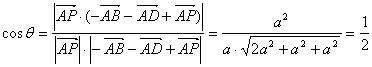∴二面角N-MD-C的大小为60°. …………………… (12分)
21．解：（1）设从2002年起的第
年（2002年为第一年），该村的人均产值为
，
每年人口较上年净增数为
，则
，…………………… 3分
则
， …………………………5分
当且仅当
，即
时，随着的增大而增大，
故要使该村人均产值年年都增长，那么该村每年人口的净增不超过16人．……７分
（另法：由
恒成立求解）
（2）由2002年该村的人均产值为
万元;
2012年该村的人均产值为
万元，………………………………… 9分
从而
,
故到2012年该村能够实现年人均产值较2002年翻一番的经济发展目标．……12分
22．解：(1)由题意
，设
（
），由余弦定理
得
．………… 4分
又
·
，
当且仅当
时，·
取最大值，
此时
取最小值
，令
，解得
，
，∴
，故所求
的轨迹方程为
．………… ７分
（2）设
，
，则由
，可得
，故
，………………………………… 9分
∵
、
在动点的轨迹上，故
且
，
消去
可得
，解得
，…………………… 12分
又
，∴
，解得
，
故实数
的取值范围是
．……………………………………………… 14分
（其他解法及评分标准略）