|
|
学科:数学 |
| 教学内容:高三数学综合测试题 |
【同步达纲练习】
一、填空题(4分×12)
1.若![]() ,则
,则![]()
2.已知集合![]() ,B={x(x-k)(x-k-1)≤0},且A∩B≠φ,则k的取值范围是_________。
,B={x(x-k)(x-k-1)≤0},且A∩B≠φ,则k的取值范围是_________。
3.已知两空间向量![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角的度数是______________。
的夹角的度数是______________。
4.已知![]() ,α在第二象限,则
,α在第二象限,则![]() 的值等于_________。
的值等于_________。
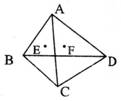
5.如图,A—BCD是一体积为![]() 的正四面体,连结两个面的重心E、F,则线段EF的长是_____________。
的正四面体,连结两个面的重心E、F,则线段EF的长是_____________。
6.已知![]() 的展开式的第7项为
的展开式的第7项为![]() ,则
,则![]() 的值是_____。
的值是_____。
7.各项均为正数的等比数列![]() 中,已知
中,已知![]() ,则
,则
![]() 的值是___________。
的值是___________。
8.若复数z满足![]() ,则复数z+1+I的模的最大值是_________。
,则复数z+1+I的模的最大值是_________。
9. 现从某校5名学生干部中选出4人分别参加上海市“资源”、“生态”和“环保”三个夏令营,要求每个夏令营活动至少有选出的一人参加,且每人只参加一个夏令营活动,则不同的参加方案的种数是_______________。(写出具体数字)
10.对于直线l上任一点P(x,y),作一变换![]() ,
,![]() ,点
,点![]() 仍在此直线上,则直线l的方程是_____________________。
仍在此直线上,则直线l的方程是_____________________。
11.老师给出一个函数y=f(x),四个学生甲、乙、丙、丁各指出这个函数的一个性质:
甲:对于x∈R,都有f(1+x)=f(1-x);
乙:在(一∞,0]上函数递减;
丙:在(0,+∞)上函数递增;
丁:f(0)不是函数的最小值。
如果其中恰有三人说得正确,请写出一个这样的函数_________。
12.等差数列![]() 中,
中,![]() 是它的前n项的和,且
是它的前n项的和,且![]() ,
,![]() 给出下列命题:
给出下列命题:
①数列![]() 中前7项是递增的,从第8项开始递减;
中前7项是递增的,从第8项开始递减;
②![]() 一定小于
一定小于![]() ;③
;③![]() 是各项中最大的;④
是各项中最大的;④![]() 不一定是
不一定是![]() 的最大值;
的最大值;
其中正确的命题的序号是__________(注:把你认为正确的命题的序号都填上)
二、选择题:(4分×4)
13.给出以下四个命题:
①若a、b是异面直线,b、c是异面直线,则a、c也是异面直线;
②若一条直线与两个平面所成的角相等,则这两个平面平行;
③若一个二面角的两个面与另一个二面角的两个面分别垂直,则这两个二面角相等或互补:
④三个平面两两相交,有三条交线,则三条交线交于一点。
其中正确命题的个数是 ( )
A.0 B.1
C.2 D.3
14.把函数y=sinx的图象上的每一个点都沿着向量![]() 的方向移动
的方向移动![]() 个单位,所得点的轨迹方程是(
)
个单位,所得点的轨迹方程是(
)
A.![]() B.
B.![]()
![]() D.
D.![]()
15.有四个命题:
①α、β是复数,且![]() ,则α=β=0
,则α=β=0
②复数Z为纯虚数的充要条件是![]() ;
;
③![]() 、
、![]() 是复数,则
是复数,则![]() 一定是实数;
一定是实数;
④若![]() 、
、![]() 都是非零复数,
都是非零复数,![]() ≠
≠![]() ,且复平面上,O为原点,点A和点B分别与
,且复平面上,O为原点,点A和点B分别与![]() +
+![]() 和
和![]() -
-![]() 对应,∠AOB=90°,则
对应,∠AOB=90°,则![]() =
=![]() ;
;
上述命题正确的是 ( )
A.②③ B.②④
C.③④ D.①③④
16.设f(x)是定义在实数集R上的函数,且满足下列关系:f(5+x)=f(5-x),f(10-x)=-f(10+x),则f(x)是 ( )
A.偶函数,又是周期函数 B.偶函数,但不是周期函数
C.奇函数,又是周期函数 D.奇函数,但不是周期函数
三、解答题:
17.(12分)设a、b、c分别为△ABC的边BC、CA、AB的长,且![]() ,若
,若![]() ,求m的值。
,求m的值。
18.(12分)给定![]() ,定义使
,定义使![]() 为整数的数k(k∈N)叫做企盼数,试求区间(1,2001)内的所有企盼数的和M。
为整数的数k(k∈N)叫做企盼数,试求区间(1,2001)内的所有企盼数的和M。
19.(15分)斜三棱柱![]() 的两底面为等腰直角三角形,直角边AB=AC=6,又
的两底面为等腰直角三角形,直角边AB=AC=6,又![]() ,
,![]() ,侧棱
,侧棱![]() 与平面
与平面![]() 成60°角,
成60°角,
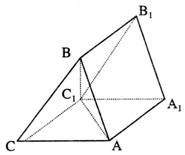
(1)求证:平面ABC⊥平面![]() ;
;
(2)求BC与平面![]() 所成的角;
所成的角;
(3)求这个三棱柱的体积。
20.(15分)据2000年4月份的“光明日报”报道,水土流失是我国西部大开发中最突出的生态问题,全国9100万亩的25度以上的坡耕地需要退耕还林,其中西部地区占70%。国家确定2000年底在西部地区退耕土地面积为515万亩,以后每年退耕土地面积递增12%。
(1)试问从2000年起,到哪一年底西部地区基本解决退耕还林问题?(用四舍五入精确到年)
(2)为支持退耕还林工作,国家财政补助农民每亩300斤粮食,每斤粮食按0.70元折算,并且每亩耕地每年补助20元。试问:到西部地区基本解决退还耕还林问题时,国家财政共需支付约多少亿元?(用四舍五入精确到亿元)。
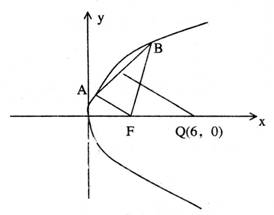
21.(16分)设抛物线C:![]() 上有两动点A、B(AB不垂直于x轴),F为焦点,且AF+BF=8,又线段AB的垂直平分线恒过x轴上定点Q(6,0),
上有两动点A、B(AB不垂直于x轴),F为焦点,且AF+BF=8,又线段AB的垂直平分线恒过x轴上定点Q(6,0),
(1)求抛物线C的方程;
(2)求△AQB的面积的最大值。
22.(16分)对于在区间[m,n]上有意义的两个函数f(x)与g(x),如果对任意x∈[m,n],均有f(x)-g(x)≤1,则称f(x)与g(x)在[m,n]上是接近的,否则称f(x)与g(x) 在[m,n]上是非接近的。
现有两个函数![]() 与
与![]() ,
,
(1)求![]() 的定义域;
的定义域;
(2)若![]() 与
与![]() 在整个给定区间[a+2,a+3]上都有意义,
在整个给定区间[a+2,a+3]上都有意义,
①求a的取值范围;
②讨论![]() 与
与![]() 在给定区间[a+2,a+3]上是否是接近的。
在给定区间[a+2,a+3]上是否是接近的。

参考答案
【同步达纲练习】
一、填空题(4分×12)
1.02.R<-6或k>2 3.90°4.![]() 5.2
5.2
6.![]() 7.20018.
7.20018.![]() 9.180
9.180
10.x+2y=0或x+y=0
11.丙:![]() 或y=x-1,甲
或y=x-1,甲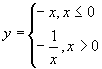
12.②③
二、选择题:(4分×4)13.A14.B15.C16.C
三、解答题:
17.解: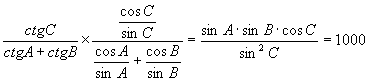 (4分)
(4分)
由正弦定理:![]() ,∴
,∴![]() (7分)
(7分)
由余弦定理:![]() (10分)∴
(10分)∴![]()
∵![]() ,∴m=2001(12分)
,∴m=2001(12分)
18.解:![]()
为整数,(4分)
∴![]() ,m∈N ∵k∈(1,2001)∴R+2∈(3,2003)
,m∈N ∵k∈(1,2001)∴R+2∈(3,2003)
∴![]() (6分)
(6分)
∴![]() ,
,
∴![]() (8分)
(8分)
![]()
19.解:(1)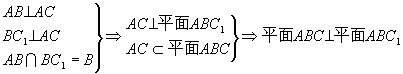 (4分)
(4分)
(2)![]() ,∴
,∴![]() ,
,![]() 中,AC=6,∴
中,AC=6,∴![]() ,
,![]() 中,
中,
![]()
∴![]() ,∴
,∴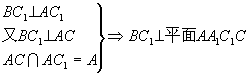 ,
,
![]() 是BC与平面
是BC与平面![]() 所成的角。而
所成的角。而![]() ,
,
∴![]() ,(8分)∴
,(8分)∴![]() ∴BC在平面
∴BC在平面![]() 所成的角为
所成的角为![]() (10分)
(10分)
(3)![]() ,
,![]()
∴![]() (15分)
(15分)
20.解:(1)设从2000年起,第几年西部地区基本解决退耕还林问题。
![]() (4分)
(4分)
![]()
=6370,![]() ∴n=8 答:从2000年起,到2007年底西部地区基本解决退耕林问题。
∴n=8 答:从2000年起,到2007年底西部地区基本解决退耕林问题。
(2)每亩耕地国家财政补贴300×0.70+20=230元。(8分)共支付:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
答:到西部地区基本解决退耕还林问题时,国家财政共需交付约570亿元。
21.解:(1)设A、B两点![]() ,
,![]() ,
,![]() ∴
∴![]() ,
,![]() ∴
∴![]() (4分)又线段AB的垂直平分线恒过定点Q(6,0)
(4分)又线段AB的垂直平分线恒过定点Q(6,0)
∴AQ=BQ![]() 又
又![]() ,
,![]()
∴![]() ∵
∵![]()
∴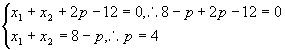
∴抛物线e的方程:![]() (8分)
(8分)
(2)∵![]() ,设AB的中点为
,设AB的中点为![]() ,
,![]() ,
,
![]()
![]() (10分)
(10分)
∴AB的方程:![]() ,∴
,∴![]() ,
,
代入![]() ,∴
,∴![]()
![]() ,∴
,∴![]() ,
,![]()
![]()
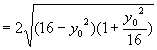
![]()
点Q到AB的距离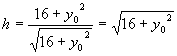 ,
,
∴![]()
(14分)![]() ,当且仅当
,当且仅当![]() 即
即![]() 时,
时,
![]() (16分)
(16分)
22.解:(1)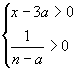 ,∴x>3a,∴
,∴x>3a,∴![]() 的定义域x∈(3a,+∞)(2分)
的定义域x∈(3a,+∞)(2分)
(2)① 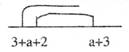
![]()
②![]() 。
。
∴设![]() 0<a<1(6分)
0<a<1(6分)
![]() u(a)在[a+2,a+3]上是单调递增的
u(a)在[a+2,a+3]上是单调递增的
∵c<a<1,∴g(a)在[a+2,a+3]上是单调递减的。
∴![]() (8分)
(8分) ![]() (10分)
(10分)
满足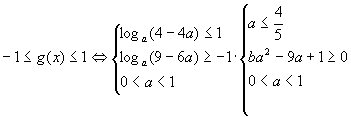 (12分)
(12分)
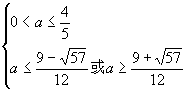 ,∴
,∴![]() (14分)
(14分)
∴当![]() 时,
时,![]() 与
与![]() 在[a+2,a+3]上是接近的。(15分)
在[a+2,a+3]上是接近的。(15分)
当![]() 且a≠1时,
且a≠1时,![]() 与
与![]() 在[a+2,a+3]上是半接近的。(16分)
在[a+2,a+3]上是半接近的。(16分)
