高三第四次月考数学试题
第Ⅰ卷(选择题部分,共12小题,总分60分)
一、选择题:每小题只有一个选项正确,每小题5分。
![]() 1、与向量
1、与向量![]() 平行的单位向量一定是( )
平行的单位向量一定是( )
A.![]() B.
B.![]() 或
或![]()
C.![]()
![]() D.
D.![]() 或
或![]()
2、已知![]() 是
是![]() 上的增函数,
上的增函数,![]() 是函数
是函数![]() 图象上两点,那么不等式
图象上两点,那么不等式![]() 的解集的补集为( )
的解集的补集为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3、条件![]() 是两条直线
是两条直线 ![]() 和
和![]() 平行的( )
平行的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
![]() 4、将曲线
4、将曲线![]() ,(
,(![]() 为常数 )按向量
为常数 )按向量![]() 平移后,得到曲线的方程是( )
平移后,得到曲线的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5、三个实数![]() 成等比数列,且
成等比数列,且![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D. ![]()
6、过点A(1,3)作直线![]() ,若
,若![]() 经过点(a,0)和(0,b)且a,b∈N*,则可作出的不同直线
经过点(a,0)和(0,b)且a,b∈N*,则可作出的不同直线![]() 的条数为( )
的条数为( )
A.1 B.2 C.3 D.多于3
![]()
![]()
![]() 7、已知向量
7、已知向量![]() ,
,![]() (O为原点,
(O为原点,![]() ),则向量
),则向量![]() 的长度的最大值是( )
的长度的最大值是( )
A.![]() B.2
B.2![]() C.3
C.3![]() D.4
D.4![]()
8、已知实数p、q满足![]() ,则p可取值的范围是( )
,则p可取值的范围是( )
A.0<p≤1 B.p≤1 C.0≤p≤1 D.p≥1
![]()
![]()
![]() 9、设O为△ABC的三个内角平分线的交点,当AB=AC=5,BC=6时,
9、设O为△ABC的三个内角平分线的交点,当AB=AC=5,BC=6时,![]() (
(![]() ),则
),则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、设![]() ,且变量x,y满足条件
,且变量x,y满足条件![]() 则t的最大值、最小值依次是( )
则t的最大值、最小值依次是( )
A.3,-3 B.5,-5 C.7,-7 D.9,-9
11、已知常数![]() ,则不等式
,则不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
12、已知关于x、y的方程组![]() 至多有一解,则实数a,m满足的关系是( )
至多有一解,则实数a,m满足的关系是( )
A.![]() 或
或![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(非选择题部分,共90分)
二、填空题:每小题4分,共16分
13、设a、b、c分别是△ABC的∠A、∠B、∠C的对边边长,则直线![]() 与直线
与直线![]() 的夹角大小是
。
的夹角大小是
。
14、不等式![]() 的解集是
。
的解集是
。
其中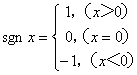
15、已知函数![]() 的定义域为R,值域为[-1,4],则a2+b2=
。
的定义域为R,值域为[-1,4],则a2+b2=
。
16、北京市为成功举办2008年奥运会,决定从2004年到2007年间更新市内现有的全部出租车。若每年更新的车辆数比前一年递增10%,则2004年底更新现有总车辆数的x%,则整数x等于 (参考数据1.14=1.46,1.15=1.61)
三、解答题(共6个小题,总分74分)
|
|
文科生作:已知不等式![]() (
(![]() 为常数)对
为常数)对![]() 恒成立,
恒成立,
解不等式:![]()
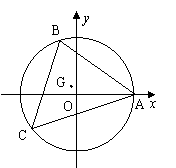 18、(12分)在圆
18、(12分)在圆![]() 上取一定点
上取一定点![]() 和两个动点
和两个动点![]() ,若
,若![]() 两点运动时,恒有
两点运动时,恒有![]() ,求
,求![]() 重心
重心![]() 的轨迹方程。
的轨迹方程。
19、(12分)已知数列![]() 的前
的前![]() 项和
项和![]() ,对任意正整数
,对任意正整数![]() 总有
总有![]() (p为常数,且
(p为常数,且![]() ,数列
,数列![]() 中有
中有![]() (
(![]() 为常数)
为常数)
(1) 求数列![]() 的通项公式;
的通项公式;
(2) 若![]() ,求p的取值范围。
,求p的取值范围。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 20、(12分)已知二次函数
20、(12分)已知二次函数![]() 对任意
对任意![]() ,都有
,都有![]() 成立,设向量
成立,设向量![]() ,
,![]() ,当
,当![]() 时,求不等式
时,求不等式![]() 的解集。
的解集。
21、(12分)在小河l同侧有两个村庄A、B,两村庄计划于河上共建一水电站发电供两村使用,已知A、B到河边垂直距离AA′、BB′分别为300m和700m,且两村A、B相距500m,(如图)问水电站建于A′B′上距A′多少m处,送电到A、B两村电线用料最省?
 |
22、(14分)已知二次函数![]()
(1)对于x1, x2∈R,且![]() 求证:方程
求证:方程![]() 有两个不等的实根,且必有一个实根属于(x1,x2);
有两个不等的实根,且必有一个实根属于(x1,x2);
|
高三第四次月考数学参考答案
一、选择题:1—5 B D B A D 6—10 B B A D C 11—12 D C
二、填空题:13、![]() 14、(
14、(![]() )∪(0,+∞) 15、13
16、22
)∪(0,+∞) 15、13
16、22
三、解答题
17(12分)理科题:证明:由已知![]()
∵![]() ∴-1<a<1 1-a2>0,同理 1-b2>0,
…………4分
∴-1<a<1 1-a2>0,同理 1-b2>0,
…………4分
∴![]() ………10分
………10分
|
文科题:解:∵![]() >0 对
>0 对![]() 恒成立,
恒成立,
∴△=![]() …………4分
…………4分
又![]() ,原不等式化为
,原不等式化为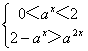
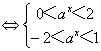 ,
∴
,
∴![]() ∴
∴![]()
∴原不等式解集为![]() ……………12分
……………12分
18、(12分)解:连接OB、OC,∵∠BAC=60°,∴∠BOC=120°
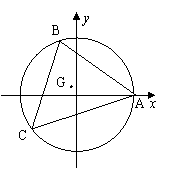 设线段BC的中点为M(
设线段BC的中点为M(![]() ),则
),则![]() ∴
∴![]() …5分
…5分
![]()
|
|
∴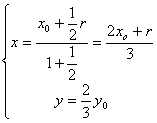 ,∴
,∴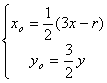 ………………10分
………………10分
代入①得所求轨迹方程为![]() ………………12分
………………12分
19、(12分)解:(1)![]() ∵
∵![]() ∴
∴![]() 2分
2分
当n≥2时,![]()
∴![]()
∴![]() 公比为
公比为![]() 的等比数列
∴
的等比数列
∴![]() ……6分
……6分
(2)由已知,得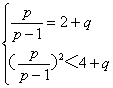 消去q,得
消去q,得
![]()
又![]() ∴p的取值范围是
∴p的取值范围是![]() ∪
∪![]() ∪(2,+
∪(2,+![]() )
………12分
)
………12分
20、(12分)解:设![]() 二次项系数为m,∵对任意x,都有
二次项系数为m,∵对任意x,都有
![]() ∴
∴![]() 的图象关于直线
的图象关于直线![]() 对称 ………2分
对称 ………2分
(1)若![]() ,则
,则![]() 在[1,
在[1,![]() )上为增函数
)上为增函数
![]()
![]() ∵
∵![]()
![]()
![]()
![]() …………4分
…………4分
![]()
![]()
![]()
![]()
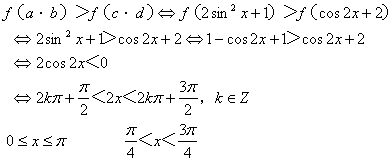 ∴
∴
![]()
∵ ∴ …………8分
(2)当![]() 时,
时,![]() 在上[1,
在上[1,![]() )是减函数
)是减函数
同理可得![]() …………10分
…………10分
综上:所求解集是当![]() 时为
时为![]()
当![]() 时为
时为![]() …………12分
…………12分
21、(12分)解:以l为x轴,A′为原点建立直角坐标系如图,设A关于x轴的对称点为A″,连A″B,设交x轴于点P.则P点为所求点,即![]() 最小,(若P′为l上任一点,则
最小,(若P′为l上任一点,则
AP′+BP′=A″P′+BP′≥A″B=AP+PB …………5分
|
|

 由已知A(0,300),A″(0,-300)
由已知A(0,300),A″(0,-300)
|
|
|
|
|
|
|
|
由两点式得A″B的方程为![]() ,令y = 0得x=90,
,令y = 0得x=90,
即OP=90 …………11分
答:水电站应建在A′B′上距A′90m处,用料最省。 …………12分
22、解:
(1) 由![]() 得
得
![]() …………2分
…………2分
由![]() ,故此方程判别式
,故此方程判别式
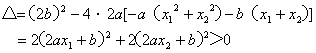
∴△>0
∴方程![]() 有两个不等的实根 ……4分
有两个不等的实根 ……4分
令![]() 是二次函数,由
是二次函数,由
![]() =
=![]() …………6分
…………6分
∵![]() ∴
∴![]()
∴![]() 的根必有一个属于(x1,x2)
…………8分
的根必有一个属于(x1,x2)
…………8分
(2)由题设,得![]() 即有
即有
![]()
∵![]() 成等差数列
成等差数列
∴![]() ,即
,即![]()
∴![]() …………10分
…………10分
故![]()