高三第四次月考数学参考答案
一、选择题:1—5 B D B A D 6—10 B B A D C 11—12 D C
二、填空题:13、![]() 14、(
14、(![]() )∪(0,+∞) 15、13
16、22
)∪(0,+∞) 15、13
16、22
三、解答题
17(12分)理科题:证明:由已知![]()
∵![]() ∴-1<a<1 1-a2>0,同理 1-b2>0,
…………4分
∴-1<a<1 1-a2>0,同理 1-b2>0,
…………4分
∴![]() ………10分
………10分
|
文科题:解:∵![]() >0 对
>0 对![]() 恒成立,
恒成立,
∴△=![]() …………4分
…………4分
又![]() ,原不等式化为
,原不等式化为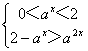
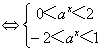 ,
∴
,
∴![]() ∴
∴![]()
∴原不等式解集为![]() ……………12分
……………12分
18、(12分)解:连接OB、OC,∵∠BAC=60°,∴∠BOC=120°
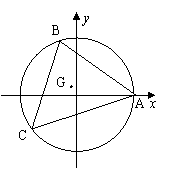 设线段BC的中点为M(
设线段BC的中点为M(![]() ),则
),则![]() ∴
∴![]() …5分
…5分
![]()
|
|
∴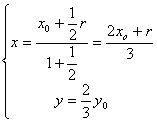 ,∴
,∴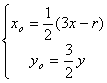 ………………10分
………………10分
代入①得所求轨迹方程为![]() ………………12分
………………12分
19、(12分)解:(1)![]() ∵
∵![]() ∴
∴![]() 2分
2分
当n≥2时,![]()
∴![]()
∴![]() 公比为
公比为![]() 的等比数列
∴
的等比数列
∴![]() ……6分
……6分
(2)由已知,得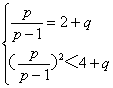 消去q,得
消去q,得
![]()
又![]() ∴p的取值范围是
∴p的取值范围是![]() ∪
∪![]() ∪(2,+
∪(2,+![]() )
………12分
)
………12分
20、(12分)解:设![]() 二次项系数为m,∵对任意x,都有
二次项系数为m,∵对任意x,都有
![]() ∴
∴![]() 的图象关于直线
的图象关于直线![]() 对称 ………2分
对称 ………2分
(1)若![]() ,则
,则![]() 在[1,
在[1,![]() )上为增函数
)上为增函数
![]()
![]() ∵
∵![]()
![]()
![]()
![]() …………4分
…………4分
![]()
![]()
![]()
![]()
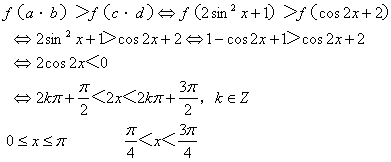 ∴
∴
∵ ∴ …………8分
(2)当![]() 时,
时,![]() 在
在![]() 上是减函数
上是减函数
同理可得![]() …………10分
…………10分
综上:所求解集是当![]() 时为
时为![]()
当![]() 时为
时为![]() …………12分
…………12分
21、(12分)解:以l为x轴,A′为原点建立直角坐标系如图,设A关于x轴的对称点为A″,连A″B,设交x轴于点P.则P点为所求点,即![]() 最小,(若P′为l上任一点,则
最小,(若P′为l上任一点,则
AP′+BP′=A″P′+BP′≥A″B=AP+PB …………5分
|
|

 由已知A(0,300),A″(0,-300)
由已知A(0,300),A″(0,-300)
|
|
|
|
|
|
|
|
由两点式得A″B的方程为![]() ,令y = 0得x=90,
,令y = 0得x=90,
即OP=90 …………11分
答:水电站应建在A′B′上距A′90m处,用料最省。 …………12分
22、解:
(1) 由![]() 得
得
![]() …………2分
…………2分
由![]() ,故此方程判别式
,故此方程判别式
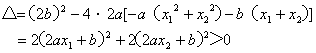
∴△>0
∴方程![]() 有两个不等的实根 ……4分
有两个不等的实根 ……4分
令![]() 是二次函数,由
是二次函数,由
![]() =
=![]() …………6分
…………6分
∵![]() ∴
∴![]()
∴![]() 的根必有一个属于(x1,x2)
…………8分
的根必有一个属于(x1,x2)
…………8分
(2)由题设,得![]() 即有
即有
![]()
∵![]() 成等差数列
成等差数列
∴![]() ,即
,即![]()
∴![]() …………10分
…………10分
故![]()
∵![]() ∴
∴![]() 故
故![]() ……………14分
……………14分