高三年级第一次月考数学试卷
一． 选择题(每小题5分，共60分)
1．如图：从集合
到集合
的映射为
，则
的值为
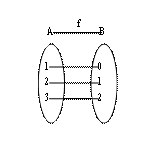（A）0 (B)1 (C)2 (D)3
2. 设全集U=R，集合M={xô
}，N={xôlogx7>log37},
那么M∩(CUN)是 （ ）
A．{xôx<-2} B．{xôx<-2或x≥3}
C．{xôx≥3} D．{xô-2≤x<3}
3．已知x
R，y R＋，集合A＝｛x2＋x＋1，－x，－x－1｝，
集合B＝｛－y，-
，y＋1｝，若A＝B，则x2＋y2
的值是
（ ）．
（A）5 （B）4 （C）25 （D）10
4．关于x的二次方程x2＋（a2－1）x＋a－2＝0的一个根比1大，另一个根比1小的充要条件是（ ）．
（A）－1＜a＜1 （B）a＜－1或a＞1
（C）－2＜a＜1 （D）a＜－2或a＞1
5．若loga2 ＜logb2 ＜0，则（ ）．
（A）0＜a ＜b ＜1 （B）0＜b ＜a ＜1
（C）a ＞b ＞1 （D）b ＞a ＞1
6. 已知函数
为偶函数，则在区间
上是（ ）
A. 增函数 B. 偶函数
C. 部分为增函数，部分为减函数 D. 无法确定增减性
7．设
，
，若的值域也是A，则b的值是
（ ）
A. 
B.
C.
D.
8．将函数
的图象C向左平移一个单位后，得到y=f(x)的图象
，若曲线关于原点对称，那么实数a的值为（ ）
（A）1 （B）-1 （C）0 （D）-3
9．商店某种货物进价下降8%，但销售价没变，于是这种货物的销售利润率［销售利润率=（销售价－进价）÷进价×100%］由原来的r%增加到(r+10)%,那么r的值为
A．12 B．15 C．25 D．50
10．函数y＝
的反函数为
(
) 则
( )
A.是奇函数，它在（0，＋∞）上是减函数
B.是偶函数，它在（0，＋∞）上是减函数
C. 是奇函数，它在（0，＋∞）上是增函数
D. 是偶函数，它在（0，＋∞）上是增函数
11．已知函数
，则
的图象可能是
 |
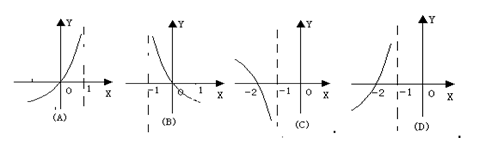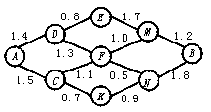12.如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相连，连线上标注的数字表示某信息经过该段网线所需的时间(单位：毫秒).信息由结点A传递到结点B所需的最短时间为( )
A.5毫秒 B.4.9毫秒
C.4.8毫秒 D.4.7毫秒
二．填空题(每小题4分，共16分)
13．集合A={2,4,a3-2a2-a+7},B={1,a+1,a2-2a+2,-0.5(a2-3a-8),a3+3a+7},且A∩B={2,5}，则实数a=__________。.
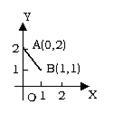14．设函数
是最小正周期为2的偶函数，它在区间[0，1]上的图象为如图所示的线段AB，则在区间[1，2]上，=
。
15．(理科)若a＞0,b＞0，且a+2b=3,则
的最小值为____________。
16．读下列命题，请把正确命题的序号都填在横线上 .
①若函数对定义域中的x总有
是偶函数；
②函数
的图象关于直线x=2对称；
③函数
的图象关于直线
对称；
④函数
的反函数的图象关于点（－2，－1）中心对称.
高三年级第一次月考数学试卷
一、选择题 (每小题3分，共36分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(每小题4分，共16分)
13________________ 14_______________________
15________________ 16_______________________
三、解答题
17．已知集合A={xx2-3x-10≤0}，B={xm+1≤x≤2m-1},若A∪B=A 求实数m的取值范围。
18．设
，解关于
的不等式，
19．（本小题12分）
某农工贸集团开发的养殖业和养殖加工业的年利润分别为
和
（万元），养殖业年利润与投入的资金
（万元）的关系是
，养殖加工业的年利润与投入的资金（万元）的关系是
。该集团今年计划对这两项生产投入资金共60万元，为获得最大利润，对养殖业与养殖加工业生产每项投入多少万元？最大利润可获多少万元？
20．定义在区间（－1,1）上的函数f(x)满足：①对任意x、y∈（－1,1）都有f(x)+f(y)=f();②当x∈（－1,0）时，f(x)>0.
（Ⅰ）求证：f(x)为奇函数；
（Ⅱ）试解不等式f(x)+f(x-1)>f().
21．（本题满分13分）
已知f（x）＝loga
（a ＞0，a ≠1）．
（1）求f（x）的定义域；
（2）判断f（x）的单调性，并予以证明；
（3）求使f（x）＞0的x取值范围．
22．（本小题满分12分）
设是f(x)定义域在[-1，1]的奇函数，
（c为常数）
①求g(2)的值及常数C；
②求f(x)的表达式；
③任意的
高三年级第一次月考数学试卷参考答案
时量：120分钟 总分：150分 命题人：张杨柳
二．选择题(每小题5分，共60分)
D B A C B A C B B C D C
三．填空题(每小题4分共16分)
13．a=2 14. 
15. 
16. 答： ③④
四．解答题
17． 答：m∈(-∞，3)
18． 解：原不等式等价于不等式组
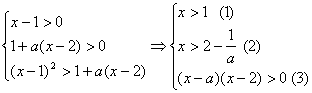
当
且
。
当
。
当
，故此时不等式组的解为
。
19． 答：当对养殖业投入25万元，对养殖加工业投资35万元时，可获最大利润约为11.67万元。
20．解：（Ⅰ）令x=y=0,则f(0)+f(0)=f(0),∴f(0)=0.
又令x∈（－1,1），则-x∈（－1,1），而f(x)+f(-x)=
∴f(-x)=-f(x),即f(x)在（－1,1）上是奇函数.
（Ⅱ）令－1<x1<x2<1,则x1-x2<0,1-x1x2>0,
于是f(x1)-f(x2)=f(x1)+f(-x2)=f()>0,即f(x1)>f(x2),所以f(x)在定义域上为减函数.从而f(x)+f(x-1)>f()等价与不等式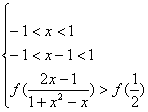
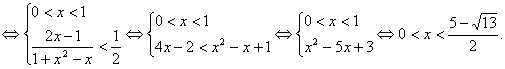
21．【略解】（1）∵ ＞0，∴ f（x）定义域为（－1，1）．
（2）设－1＜x1＜x2＜1，则
f（x1）－f（x2）＝loga
－loga
＝loga
＝loga
∵ －1＜x1＜x2＜1，∴ x2－x1＞0，
∴ （1－x1x2）＋（x2－x1）＞（1－x1x2）－（x2－x1）
即
＜1．
∴ 当a ＞1 时，f（x1）＜f（x2），在（－1，1）上是增函数．
当0＜a ＜1时，f（x1）＞f（x2），在（－1，1）上是减函数．
（3）当a ＞0时，欲f（x）＞0，则有＞1，解得0＜x＜1．
当0＜a ＜1时，欲f（x）＞0，则有0＜＜1，解得－1＜x＜0．
22．解：①
②由①
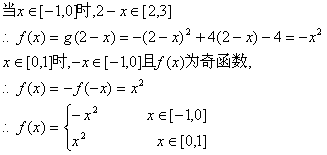
③
