高三年级质量检测(二) 数学试题
本试卷满分150分，考试时间120分钟.
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分
1．如果cos2θ=
, 则sinθ 等于 （ ）
A．
B．
C．
D．
2．等比数列{an}的前n项的和为Sn，已知a5=2S4+3, a6=2S5+3，则数列的公比q等于（ ）
A．2 B．3 C．4 D．5
3．已知球的两上平行截面的面积分别为5π和8π，它们位于球心的两则，且相距为3那么球面积为 （ ）
A．65π B．36π C．16π D．100π
4．已知f(x)=x2－2x+5, g(x)=f(2－x2)，那么g(x) （ ）
A．在区间(－1,0)上是增函数 B．在区间(0,1)上是增函数
C．在区间(－2,0)上是减函数 D．在区间(0,2)上是减函数
5．如果α、β∈
，则
（ ）
A．tanα<cotβ,tanβ<cotα B．anα>cotβ,tanβ<cotα
C．tanα<cotβ,tanβ>cotα D．tanα>cotβ,tanβ>cotα
6．设有三个命题 （ ）
甲：相交两直线l，m都在平面α内，并且都不在平面β内；
乙：l, m之一至少有一条与β相交
丙：α与β相交。 则在甲成立时
A．乙是丙的充分不必要条件 B．乙是丙的必要不充分条件
C．乙是丙的充分必要条件 D．乙是丙的既不充分又不必要条件
7．如果椭圆的焦距是8，焦点到相应的准线的距离为9/4，则椭圆的离心率为 （ ）
A．
B．
C．
D．－
8．二项式
的展开式中的有理项(既x的幂指数是整数的项)共有 （ ）
A．1个 B．2个 C．3个 D．4个
9．若实数x,y满足(x+5)2+(y+12)2=142，则x2+y2的最小值是 （ ）
A．2 B．1 C．3 D．4
10．马路上有编号为1,2，…，9,10的10只灯，为节约用电，可以关掉其中3只，但两端1和10号灯不能熄，也不能关掉相邻的两只或三只，共有关灯方法 （ ）
A．C35 B．C36 C．C37 D．C310
11．正方体ABCD－A1B1C1D1中，E是BC的中点，则A1C与DE所成的角的余弦为（ ）
A．
B．
C．
D．
12．有3个命题
（1）底面是正三角形，其余各个面都是等腰三角形的棱锥是正三棱锥；
（2）各个侧面都是等腰三角形的四棱锥是正四棱锥；
（3）底面是正三角形，相邻两侧面所成的二面角都相等的三棱锥是正三棱锥。
其中假命题的个数是 （ ）
A．0 B．1 C．2 D．3
第Ⅱ卷（非选择题，共90分）
二、填空题：本大题共4个小题，每小题4分，共16分。把答案填在题中的横线上。
13．已知两个命题，如果A是B的充分条件，那么B是A的______条件，如果A是B的充
分必要条件，那么
的__________条件。
14．如果ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE和CE折
起，使AE和BE重合，记A与B重合后的点为P，则面PCD与面ECD所成的角为____。
15．在展开式(a+b)n的二项式系数中Cn2=15，则展开式的所有项系数的和为_______。
16．同时投掷四枚均匀硬币，至少有两枚正面向上的概率是__________。
三、解答题：本大题共6个小题,共74分，解答应写出文字说明，证明过程或演算步骤。
17．（本题满分12分）有甲、乙两个篮球运动员，甲投篮的命中率为0.7，乙投篮的命中率为0.6，每人各投篮三次： （Ⅰ）甲恰有2次投中的概率；
（Ⅱ）乙至少有1次投中的概率；
（Ⅲ）甲、乙两人投中数相等的概率。
18．（本题满分12分）已知：a=（cos
,sin）b=（cos
,sin）(0＜＜＜
）
（I）求证：a+b与a－b互相垂直；
（II）若ka+b与ka－b大小相等，求－（其中k
R且k
0）
19．（本题满分12分）设倾斜角为
的直线
与中心在原点，焦点在坐标轴上，且一准线为
的椭圆C交于B、C两点，直线
过线段BC的中点M。⑴求椭圆C的方程；⑵若以椭圆C的上顶点D为直角顶点作此椭圆的内接等腰三角形DEF，试问：这样的等腰三角形是否存在？若存在，有几个？若不存在，说明理由。
20．（本题满分12分）给定一个锐角三角形纸片，其边长分别为2a,2b,2c，要求将它剪拼成一个三棱锥，使它的底面面积和三个侧面的面积均相等，请你设计一种剪拼方法，并求出其中一组对棱所成的角。
21．(本题满分12分)设整数列{an}是一个公差不为零的等差数列，a5=6.
（Ⅰ）当a3=3时，请在数列{an}中找一项am，m>5，使得a3,a5,am成等比数列；
（Ⅱ）当a3=2时，若自然数n1,n2,……,nt满足5< n1< n2<…nt<…,使得a3,a5,
是等比数列，求nt；
（Ⅲ）如果存在自然数n1,n2,……,nt满足5< n1< n2<…nt<…，使得
a3,a5, 构成等比数列，求证：12必是a3的倍数.
22．（本题满分14分）设P（p，p3）是曲线C：y=x3的一点，过点P引曲线C的切线，将切线以P 为中心逆时针方向旋转45°，得到直线．
（1）求直线的方程；
（2）若与C相交于相异的3点时，求p的范围．
高三年级质量检测2答案
一、选择题
1.选C. 2.选B。3.选B.4.选A.5选C. 6.选C. 7.选A 8.选C. 9.选B. 10.选B. 11.选A. 12.选D.
二、填空题 13.必要条件,充要条件. 14.填
15.填64.
.
16.填
. 考虑反面情况,只有一枚正面向上或均为反面.
三、解答题 17.(Ⅰ)甲恰有2次投中的概率
;…3分
(Ⅱ)乙至少有1次投中的概率可视为3次独立重复试验中乙投中次数不少于1的事件发生的概率
……7分
(Ⅲ)分4种情况①甲乙均未投中;②甲乙均投中1次;③甲乙均投中2次;④甲乙均投中3次;故所求概率为
.…………12分
18. 解：（1）依题意知a+b=（cos+cos, sin+sin），a－b=（cos－cos, sin－sin） …2分
∴(a+b)(a－b)=（cos+cos）（cos－cos）+ (sin+sin)(sin－sin)
=cos2－cos2 +sin2－sin2=0……4分 ∴(a+b)⊥(a－b)……6分
(2) ∵ka+b=（kcos+cos, ksin+sin），ka－b=（kcos－cos, ksin－sin）……………7分
∴ka+b=
， ka－b=
………9分
∵ka+b=ka－b ，∴2kcos(－)=－2kcos(－)且k0 ∴cos(－)=0…………10分
又∵0＜＜＜ ∴－＜－＜0 ∴－= －
.…………12分
19. ⑴ 设椭圆C的方程为
由一准线为，得
①……………………………………1分
设B（
）、C（
）、M（
，
B、C在椭圆C上，
，
两式相减得：
，
直线BC的斜率存在
，
将
代入上式化简整理得：
，又
，
②………………………………………………4分
由①②得：
，故所求椭圆方程为：
。………………5分
⑵ 易得上顶点为D（0，1），不妨设E，F分别位于
轴的左右两侧，由于DE的斜率存在设其为
，则
，DE所在直线方程为
，代入椭圆方程化简并整理得：
（1+4
）
，………………………………………7分
E的横坐标为
，DE=
，
同理：DF=
…………………9分 由DE=DF得：
，
化简得：
（
或
………………………………………………………11分
符合题意的等腰三角形一定存在且有3个。………………………………… 12分
20.取△S1S2S3三边中点A，B，C.沿AB，BC，CA将△S1AB，△S2AC，△S3CB分别折起，使S1，S2，S3重合，……4分 记为S即可. 设AB=c, BC=a , CA=b ,下面求SA与BC所成的角. 因为S2A ∥BC，
∴∠SAS2为SA与BC所成的角或其补角.……6分 连SS1，SS2，SS3 ∵SA=S2A=S1A ∴∠S2SS1为直角， 同理∠S1SS3为直角，∠S2SS3为直角，设SS1=x, SS2=y, SS3=z，由勾股定理，
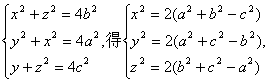……8分 在△SAS2中由余弦定理，
cos∠SAS2=
，
∴SA与BC所成的角为arccos
,……11分同理可得，SB与AC所成的角为
arccos
，SC与AB所成的角为arccos
.……12分
21. (Ⅰ)设
公差为
,则由
,得
,……2分当
时,
由
,即
,解得
,即
成等比数列;……4分
(Ⅱ)
, 当
时,
an=a3+(n－3)d=2n－4,又
成等比数列,
则
,
,
又
,
即
,8分
(Ⅲ) 
时
成等比数列, 
,即
,又是等差数列, 当
时, 
,
,
,
,
为整数,∴n1>5,
12必为a3倍数.…12分
22. ∵y / =3x2，∴过点P的切线斜率为3p2，设直线的斜率为k，则
，
∴k=
，直线的方程为y－p3 = （x－p），……6分代入y=x3，消去y，
得（x－p）[（1－3p2）x2+p（1－3p2）x－3p4－2p2－1]=0，该方程有不同的3个实数解，
亦即方程（1－3p2）x2+p（1－3p2）x－3p4－2p2－1=0有x≠p的两个相异实数解，……10分
由1－3p2≠0，得p≠
，由方程的判别式
>0，得（1－3p2）（9p4+9p2+4）>0，
∵9p4+9p2+4恒正,∴1－3p2>0，亦即
<p<
，故所求p的范围为（，）．……14分