高三年级质量检测(十一) 数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)
一.选择题(本大题共12小题,每小题5分,共60分)
1.已知集合M={a,0},N={x2x2—5x<0,x∈z},若M∩N≠![]() ,则a等于
( )
,则a等于
( )
A.1 B.2 C.1或2 D.1或![]()
2.一枚硬币连掷三次至少出现一次正面的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知f(x)=ax3+3x2+2,若f′(—1)=4,则a的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知a、b是直线,α、β、γ是平面,给出下列命题:①a∥α,a∥β,α∩β= b,则a∥b; ②α⊥γ,β⊥γ,则α∥β;③a⊥α,b⊥β, a⊥b,则α⊥β;④α∥β,β∥γ,a⊥α,则a⊥γ.其中错误的命题的序号是 ( )
A.① B.② C.③ D.④
5.已知双曲线![]() 的离心率e<2,则k的取值范围是
( )
的离心率e<2,则k的取值范围是
( )
A.k<0或k>3 B.-3<k<0 C.-12<k<0 D.-8<k<3
6.若向量![]() 则
则![]() 一定满足
( )
一定满足
( )
A.![]() 的夹角等于
的夹角等于![]() B.
B.![]() ⊥
⊥![]()
C.![]() ∥
∥![]() D.
D.![]() ⊥
⊥![]()
7.下列命题中,使命题M是命题N成立的充要条件的一组命题是 ( )
A.M:a>b; N:ac2>bc2 B.M:a>b,c>d, N:a-d >b-c
C.M:a>b>0,c>d>0, N:ac>bd D.M:a-b=a+b, N:ab≤0
8.如果一个圆锥中有三条母线两两所成的角均为60°,那么这个圆锥的侧面展开图的圆心
角等于 ( )
A.π B.![]() π C.
π C.![]() D.
D.![]()
9.圆x2+y2-4x-2y+c=0与y轴交于A、B两点,圆心为P,若∠APB=90°,则c的值为( )
A.8 B.3 C.![]() D.—3
D.—3
10.数列![]() 的前n项和为Sn,则
的前n项和为Sn,则![]() 的值等于
( )
的值等于
( )
A.1 B.0 C.2 D.![]()
11.设![]() 的反函数的解析式是 ( )
的反函数的解析式是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06(0.5·[m]+1)(元)决定,其中
m>0,[m]是大于或等于m的最小整数,(如[3]=3,[3.8]=4,[3.1]=4),则从甲地到乙地通话时间为5.5分钟的电话费为 ( )
(A)3.71元 (B)3.97元 (C)4.24元 (D)4.77元
第Ⅱ卷(非选择题 共90分)
二.填空题(本大题共4小题,每小题4分,共16分。把答案填在题中横线上)
13.某高校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设,某人必须被选
派的种数是 。
14.设抛物线y2=4x的一条弦AB以P(![]() ,1)为中点,则该弦所在直线的斜率为 。
,1)为中点,则该弦所在直线的斜率为 。
15.已知两异面直线a、b所成的角为![]() ,直线l分别与a、b所成的角都是θ,则θ的取值
,直线l分别与a、b所成的角都是θ,则θ的取值
范围是 。
16.某地区重视环境保护,绿色植被面积呈上升趋势,经调查,从1989年到1998年这10年间每两年上升2%,1997年和1998年这两年种植植被815万平方米,当地政府决定今后四年内仍按这一比例发展下去,那么从1999年到2002年种植植被面积为
(保留整数)。
三.解答题(本大题共6小题,共74分。解答应写出文字证明,证明过程或演算步骤)
17.(本小题满分12分)
已知函数![]()
(Ⅰ)试判断函数f(x)的奇偶性;
(Ⅱ)解不等式![]()
18.本小题满分12分)
已知△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若
![]() 求A、B、C的大小。
求A、B、C的大小。
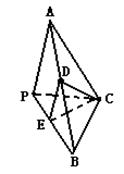
19.(本小题满分12分)在三棱锥P—ABC中,PA=a, AB=AC=![]() a,∠PAB=∠PAC=45°,
a,∠PAB=∠PAC=45°,
cos∠BPC=![]()
(Ⅰ)D是AB上任意一点(D与A、B不重合),DE⊥PB于E,求证AP∥平面DEC;
|
20.(本小题满分12分)
某生产流水线,由于改进了设备,预计第一年产量的增长率为160%,以后每年的增长率是前一年的一半。设原来的产量是a .
(Ⅰ)写出改进设备后的第一年,第二年,第三年的产量,并写出第n年与第n-1年(n≥2,n∈N)的产量之间的关系式;
(Ⅱ)由于设备不断老化,估计每年将损失年产量的5%,如此下去,以后每年的产量是否始终是逐年提高?若是,请给予证明;若不是:请说明从第几年起,产量将比上一年减少?
(21)(本小题满分12分)
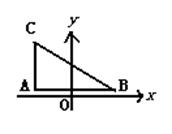
如图,在Rt△ABC中,∠BAC=90°,A(—![]() ,1)、B(
,1)、B(![]() ,1),S△ABC=
,1),S△ABC=![]() (平方单位),动点P在曲线E(y≥1)上运动,若曲线E过点C且满足PA+PB的值为常数.
(平方单位),动点P在曲线E(y≥1)上运动,若曲线E过点C且满足PA+PB的值为常数.
(Ⅰ)求曲线E的方程;
|
(22)(本小题满分14分)
设函数![]() 的定义域是x>0,若函数
的定义域是x>0,若函数
![]() 有最小值m,且m>2+
有最小值m,且m>2+![]() ,求a的取值范围.
,求a的取值范围.
高三年级质量检测11答案
一.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | C | A | B | B | C | B | D | C | D | A | B | C |
二.13.35 ; 14.2 15.[![]() ];16.1679万平方米 .
];16.1679万平方米 .
三.17.解:(Ⅰ)![]()
且![]() 内是奇孙数.…………5分
内是奇孙数.…………5分
(Ⅱ)依题意,得![]() ……………………………………………6分
……………………………………………6分
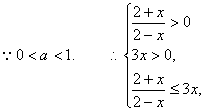 解之,得
解之,得![]() .……………………12分
.……………………12分
18.解:由![]() …………………1分
…………………1分
![]() ………………………………………3分
………………………………………3分
![]() A是△ABC的内角,
A是△ABC的内角,![]() ……………………………………5分
……………………………………5分
由正弦定理知sinB+sinC=![]() 8分
8分
|
19.(Ⅰ)证明:在△PAB中,AP=a , AB=![]() a , ∠PAB=45°,
a , ∠PAB=45°,
![]() ∠PAB
∠PAB
=![]()
![]() AP2+PB2=2a2=AB2.
AP2+PB2=2a2=AB2. ![]() △PAB是直角三角形,且AP⊥PB . 又AP、DE都在平面PAB内,且DE⊥PB,
△PAB是直角三角形,且AP⊥PB . 又AP、DE都在平面PAB内,且DE⊥PB,
![]() AP∥DE,故AP∥平面DEC.…………………………………………4分
AP∥DE,故AP∥平面DEC.…………………………………………4分
(Ⅱ甲)在 △PAC中,同(Ⅰ)理,得AP⊥PC,而PC∩PB=P,![]() AP⊥平面PBC .………………6分
AP⊥平面PBC .………………6分
又平面PAC与平面DEC有一公共点C,且AP∥平面DEC,高PAC∩平面DEC=l,则C∈l,且AP∥l .
![]() l⊥平面PBC于C .
l⊥平面PBC于C . ![]() PC⊥l,CE⊥l,从面∠PCE即为所求二面角P-l-E的平面角.…………8分
PC⊥l,CE⊥l,从面∠PCE即为所求二面角P-l-E的平面角.…………8分
在Rt△PAC中,∠PAC=45°,故PA=PC=a ,同理PB=a . 又D是AB的中点,DE∥AP,则E是PB的中点,从而PE=![]() a . 在△PEC中,cos∠BPC=
a . 在△PEC中,cos∠BPC=![]() ,PC=a , PE=
,PC=a , PE=![]() a ,
a ,
![]() ∠BPC=
∠BPC=![]()
![]() ∠PCE=
∠PCE=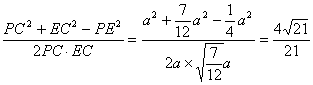
故所求二面角的余弦值为![]() .………………12分
.………………12分
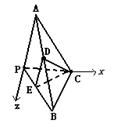
(Ⅱ乙)如图,建立空间直角坐标系. 由已知,得A、B、C三点的坐标分别为A(0,a ,0)、![]() B(
B(![]() ………………………………………………………7分
………………………………………………………7分
![]()
![]() 9分
9分 ![]() D是AB的中点,DE∥AP,
D是AB的中点,DE∥AP,![]() E是PB的中点,
E是PB的中点,
且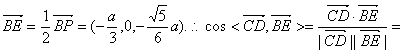
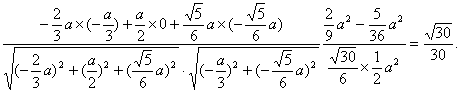 …………12分
…………12分
20.解:(Ⅰ)设第n年的产量为an ,则
a1=a(1+160%), a2=a(1+160%)(1+80%) a3==a(1+160%)(1+80%) (1+40%),………
即![]() …………………………………………………………3分
…………………………………………………………3分
![]() ………………6分
………………6分
(Ⅱ)依题意,![]() (1-5%). 若以后每年的产量逐年减少,
(1-5%). 若以后每年的产量逐年减少,
即![]() (1-5%)<1 .
(1-5%)<1 .
![]()
但22>![]() ,21<
,21<![]() ,且n≥2,n∈N,∴当n-4≥2,即n≥6时,
,且n≥2,n∈N,∴当n-4≥2,即n≥6时,![]() 故从第6年起,产量比上一年减少.………………12分
故从第6年起,产量比上一年减少.………………12分
21.(Ⅰ)解:∵AB=2![]() ,S△ABC=
,S△ABC=![]() AC·AB=
AC·AB=![]() ,∴AC=1.但BC2=AC2+AB2,从而BC=3 .
,∴AC=1.但BC2=AC2+AB2,从而BC=3 .
又PA+PB=AC+BC=4>2![]() ,∴P点在以A、B为焦点,半长轴为a=2,半焦距为c=
,∴P点在以A、B为焦点,半长轴为a=2,半焦距为c=![]() ,半短轴为b=
,半短轴为b=![]() 的椭圆E(y≥1)上.
∴曲线E的方程为
的椭圆E(y≥1)上.
∴曲线E的方程为![]() ………………6分
………………6分
(Ⅱ)设直线l:y=x+m ,代入E的方程,消x ,可得3y2-2(m+2)y +m2-2 =0 .令f(x)= 3y2-2(m+2)y +m2-2 .方程f(y)=0,有两个不小于1,且不相等的实根时,有
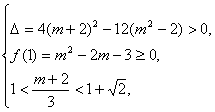 解之,得
解之,得![]() . …………9分
. …………9分
设PQ的中点为M(x ,y ),P、Q两点的坐标分别为P(x1 ,y1),Q(x2 ,y2),
![]() 将m=3y-2代入y=x+m得
将m=3y-2代入y=x+m得
y =![]() 即为M点的轨迹方程.………………………………12分
即为M点的轨迹方程.………………………………12分
22.解:![]()
即![]() ∵函数f(x),g(x)定义域为x>0,∴函数F(x)的定义域为x>0.
∵函数f(x),g(x)定义域为x>0,∴函数F(x)的定义域为x>0.
…………3分
1°当a<0时,![]() 则F(x)<2,与F(x)≥m>2+
则F(x)<2,与F(x)≥m>2+![]() 矛盾.…………5分
矛盾.…………5分
2°当0<a≤![]() 时,
时,![]() 函数F(x)在x>0上是增函数,即F(x)=m,当x<x0时,有
函数F(x)在x>0上是增函数,即F(x)=m,当x<x0时,有
F(x)< F(x0)=m与F(x)≥m 矛盾.……………………7分
3°当a≥4时,![]() 函F(x)在x>0上是减函数,即F(x0)=m ,当x>x0时,有F(x)< F(x0)=m与F(x)≥m 矛盾.……………………9分
函F(x)在x>0上是减函数,即F(x0)=m ,当x>x0时,有F(x)< F(x0)=m与F(x)≥m 矛盾.……………………9分
∴![]() <a<4,此时
<a<4,此时![]()
![]()
![]() 当且仅当
当且仅当![]()
即![]() 时,F (x)取得最小值
时,F (x)取得最小值![]() …………12分
…………12分
当m>2+![]() 时,有
时,有![]() 即
即![]() 解得
解得![]()
…………………………14分.