高考数学第一次诊断性考试

数学 (理工农医类)

本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共四页．全部解答都写在答卷(卡)上，不要写在本题单上．120分钟完卷，满分150分．

第Ⅰ卷(选择题，共60分)

注意：

1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用钢笔和4B或5B铅笔写、涂在答题卡上．

2．每小题选出答案后，用4B或5B铅笔把答题卡上对应题目的答案标号涂黑．若需改动，用橡皮擦擦干净后，再选涂其它答案，不准答在本题单上．

3．参考公式：

如果事件A、B互斥，那么P(A+B)=P(A)+P(B)；

如果事件A、B相互独立，那么P(A·B)=P(A)·P(B)；

如果事件A在一次试验中发生的概率为P，那么n次独立重复试验中恰好发生k次的概率：；

正棱锥、圆锥的侧面积公式

　其中c表示底面周长，l表示斜高或母线长；

球的体积公式 　 其中R表示球的半径．

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，把它选出来填涂在答题卡上．

1．已知集合P={－1，0，1}，Q={y︱y=sinx，x∈P}，则P∩Q是C

A．{－1，0，1}　　　 B．{0，1}　　　　  C．{0}　　　　 D．{1}

2．设两个集合A={1，2，3，4，5}，B={6，7，8}，那么可以建立从A到B的映射个数是　　　　B

A．720　　　　　　　  B．243　　　　　　　  C．125　　　　　　　  D．15

3．若不等式∣ax + 2∣＜6的解集为(－1，2)，则实数a等于　　A　

A．－4　　　　 　　　　B．4　　　　　　 　C．－8　　　　　  　　 D． 8

4．已知函数f (x)的图象恒过点(1，1)，则f (x－4)的图象过　　D

A．(－3，1)　　　　 B．(1，5)　　　　C．(1，－3)　　　　 D．(5，1)

5．已知 ，那么f (16) 等于　　D

A．4　　　　　 B．　　　　　  C．16　　　　　 D．

6．定义在实数集R上的函数y=f(－x)的反函数是，则　A

A．y=f(x)是奇函数

B．y=f(x)是偶函数

C．y=f(x)既是奇函数，也是偶函数

D．y=f(x)既不是奇函数，也不是偶函数

7．下列求导正确的是　　　B

A．　　　　　　  B．

C．=3^x·log₃e　　　　　　  D．=－2xsinx

8．设随机变量的分布列为则a的值是　 D

A．1　　　 B．　　　　  C．　　　　 　D．

9．的值为　 A

A． 2　　　　 B． 0　　　　　  C． 1　　　　　 D． 不存在

10．已知z∈C，满足不等式的点Z的集合用阴影表示为C

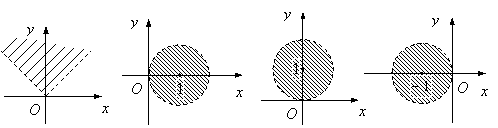A．　　　　　　　　　 B．　　　　　　　　　　 C．　　　　　　　　　　　  D．

11．甲、乙两名篮球队员轮流投篮直至某人投中为止，每次投篮甲投中的概率为0.4，乙投中的概率为0.6，且不受其它投篮结果的影响．设甲投篮的次数为，若甲先投，则　　　 B

A．　　　　　　　　　　 B．　　

C．　　　　　　　　　　 D．

12．我们用记号来表示复数cosq +isinq，即 (其中e= 2.71828…是自然对数的底数，q 的单位是弧度)．则：

① ；　　 ② ； 　　　③ ．

其中正确的式子代号为　  C

A．①　　　　　  B．①②　 　　　　　C．①③　 　　　　D．②③

第Ⅱ卷 (非选择题　 共90分)

二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．

13．一个公司有N个员工，下设一些部门，现采用分层抽样方法从全体员工中抽取一个容量为n的样本 (N是n的倍数)．已知某部门被抽取了m个员工，那么这一部门的员工数是　　　　　　　　　  ．

14．　　　　　　　  　　．－ 1　　　　

15．计算：　　　　　　　　　 ．　　－1

16．关于函数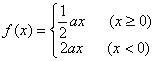，下列表述不正确的是　　　　　　　　  ．(填写答案序号)　　　　　 ① ③ ④

① 它是一个奇函数； ② 它在每一点都连续；③ 它在每一点都可导；④ 它是一个增函数； ⑤ 它有反函数．

三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．

17．(本题满分12分) 设随机变量x 服从正态分布：x ~ N(1，2²)，试求：

(Ⅰ) ；

(Ⅱ) 求常数c， 使 ．

参考数据：F(0)=0.5；F(1)=0.8413；F(2)=0.9772；F(0.5)= 0.6915；F(1.88)=0.9697；F(3)=0.9987．

17．解： (Ⅰ)　由=

==2　　　　

=2=0.3830．

(Ⅱ)　由已知可得　，

∴　 ，

即　　，

∴　 ，

∴　 ，　c=4.76．

18．(本题满分12分) 已知函数在[0，2]上有最小值8，求正数a的值．

解：设，

当x∈[0，2]时，可得．

(1) 若a＞1时，则，解得a=16＞1．

(2) 若0＜a＜1时，则，解得a=2，此与0＜a＜1矛盾，舍去．

故正数a =16．

19．(本题满分12分) 已知p：∣1－2x∣≤ 5，q：x²－4x+4－9m² ≤ 0 (m＞0)，若p是q的充分而不必要条件，求实数m的取值范围．

解：解不等式可求得：

p：－2≤x≤3，　q：2－3m≤x≤2+3m (m＞0)．

则 p：A={x∣x＜－2或x＞3}，

q：B={x∣x＜2－3m或x＞2+3m，m＞0．

由已知 p q，得AB，从而

．

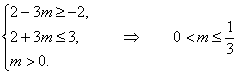(上述不等式组中等号不能同时取)．

经验证为所求实数m的取值范围．

20．(本题满分12分) 已知f(x)是定义在(－∞，0)∪(0，+∞)上的奇函数，当x＜0时，f(x)=x²－x－2，解不等式f(x)＞0．

解： 设x＞0，则 －x＜0．

∴　f (－x)=(－x)²－(－x)－2=x²+x－2．

而f (x) 是奇函数，

∴　f (－x)=－f (x)，

于是 f (x)=－x²－x+2，x＞0．

∴

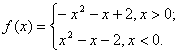
(1) 由 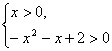　得　．

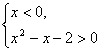(2) 由 　 得　．

综上所述，不等式f (x)＞0的解集为{x∣x＜－1或0＜x＜1．

21．(本题满分12分) 某保险公司新开设了一项保险业务，若在一年内事件E发生，该公司要赔偿a元．设在一年内E发生的概率为p，为使公司收益的期望值等于a的百分之十，公司应要求顾客交多少保险金？

解：设保险公司要求顾客交x元保险金，若以x表示公司每年的收益额，则x是一个随机变量，其分布列为：

x	x	x－a
P	1－p	p

因此，公司每年收益的期望值为

Ex=x(1－p)+(x－a)·p=x－ap．

为使公司收益的期望值等于a的百分之十，

只需Ex=0.1a，即x－ap=0.1a，

故可得x=(0.1+p)a．

即顾客交的保险金为(0.1+p)a时，可使公司期望获益10%a．

说明：当事件E发生的概率较小时，即使赔偿数目较大，保险公司仍可获益．例如当P=0.001，a=10000元时，根据上述赔偿办法，顾客只需交纳(0.1+0.001)×10000=1010元保险金，但保险公司仍可期望获益10%a=1000元，当保险公司的顾客较多时，其效益十分可观．

22．(本题满分14分) 已知函数在开区间(0，1)内是增函数．

(Ⅰ) 求实数a的取值范围；

(Ⅱ) 若数列{a_n}满足a₁∈(0，1)，，证明：．

(Ⅲ) 若数列{b_n}满足b₁∈(0，1)，，问数列{b_n}是否单调？

(Ⅰ) 解：，由于f (x)在(0，1)内是增函数，

∴ ，即 在x∈(0，1)时恒成立．

∴　 恒成立，

而　－2＜x－2＜－1，

∴　，

即　，

∴　a≥1即为所求．

(Ⅱ) 证明：由题设知，当n=1时，a₁∈(0，1)．

假设当n=k时，有a_k∈(0，1)，则

当n=k+1时，有且(由第一问知f(x)=ln(2－x)+x在(0，1)上是增函数)，

∴　n=k+1时命题成立，故0＜a_n＜1，n∈N^*．

又　∵ ，

∴　．

(Ⅲ) 数列{b_n}不具有单调性．

令 ， 则 ，

∴　 b₂＞b₁．

又　∵　 1＜b₂＜2，0＜2－b₂＜1，

∴　　ln(2－b₂)＜0，　

∴　 ．

由此表明数列{b_n}没有单调性．