高三数学第三次月考理科试卷
卷一
一、选择题(每小题5分,共60分)
1.已知函数 ![]() =
=![]() ,若
,若![]() ,则 ( )
,则 ( )
A. ![]() B.
B.![]()
C. ![]() D.
D.![]()
2. 已知角![]() 终边上一点的坐标为(
终边上一点的坐标为(![]() ),则
),则![]() 角的弧度可能为 ( )
角的弧度可能为 ( )
A.3 B.- 3 C.
![]() D.
D.
![]()
3.不等式![]()
![]() >0的解集是 ( )
>0的解集是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 集合A=![]() ,B=
,B=![]() ,且
,且![]() ,则
,则
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知函数![]() 在区间[
在区间[![]() ]上具有单调性,且
]上具有单调性,且![]()
![]() < 0,则方程
< 0,则方程![]() =0在区间[
=0在区间[![]() ]上 ( )
]上 ( )
A.至少有一个实根 B.至多有一个实根 C.无实根 D.必有唯一实根
6.设指数函数![]() ,
,![]() (
(![]() 且
且![]() )的反函数依次
)的反函数依次![]() 与
与![]() ,若
,若![]() ,则
,则![]() 与
与![]() 的图象位置关系是 (
)
的图象位置关系是 (
)
A.关于直线![]() 对称 B.关于原点对称 C.关于
对称 B.关于原点对称 C.关于![]() 轴对称 D.关于
轴对称 D.关于![]() 轴对称
轴对称
7.设![]() =
=![]() ,
,![]() =
=![]() ,使
,使![]() 为奇函数的实数m,n的可能取值为
为奇函数的实数m,n的可能取值为
( )
A.![]() B.
B.
![]()
C. ![]() D.
D.
![]()
8.将函数![]() 的图象向左平移m
的图象向左平移m![]() 个单位,所得到的图象关于y轴对称,则m的最小正值是( )
个单位,所得到的图象关于y轴对称,则m的最小正值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
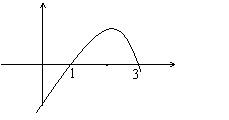
时, ![]() 的图象如图所示,那么不等式
的图象如图所示,那么不等式![]() 的解集是 ( )
的解集是 ( )
 A.
A. ![]() Y
Y
B. ![]()
|
D. ![]()
10.已知![]() ,求
,求![]() = (
)
= (
)
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
11.![]() 是定义在
是定义在![]() 上的偶函数,
上的偶函数,![]() 是定义在
是定义在![]() 上的奇函数,已知
上的奇函数,已知![]() =
=![]() ,若
,若![]() =2001,则
=2001,则![]() 的值是 ( )
的值是 ( )
A.2001 B.-2001 C.-2002 D.2002
12.已知6枝玫瑰和3枝康乃馨的价格之和大于24元,而4枝玫瑰与5枝康乃馨的价格之和小于22元,则2枝玫瑰的价格和3枝康乃馨的价格比较结果是 ( )
A.2枝玫瑰价格高 B.3枝康乃馨价格高 C.价格相同 D.不确定
卷二
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 |
| ||
| 得分 |
|
|
|
|
|
|
| |
二、填空题(每小题4分,共16分)
13.若函数![]() =
=![]() 的单调递减区间是(
的单调递减区间是(![]() ),则实数
),则实数![]() 的值为___________.
的值为___________.
14.已知: ![]() 、
、![]() 是锐角,
是锐角, ![]() =
=![]() ,
,![]() =
=![]() 则
则![]() =______________
=______________
15.若![]() 是R上的减函数,且
是R上的减函数,且![]() 的图象经过A(0,3)和B(3,-1)则不等式
的图象经过A(0,3)和B(3,-1)则不等式
![]() <2的解集是_________________________.
<2的解集是_________________________.
16.有下列命题:①
![]() 成等比数列的充分但非必要条件;
成等比数列的充分但非必要条件;
②
若角![]() 满足
满足![]() 则
则![]() ;
;
③ 若不等式![]() 的解集非空,则必有
的解集非空,则必有![]()
④ 函数![]()
![]() 的值域是[-2,2].
的值域是[-2,2].
其中错误的命题的序号是 (把错误的命题的序号都填上)
三、解答题
17.(12分)已知![]() , (
, (![]() ),求
),求![]() 的值
的值
18.(12分)解不等式![]()
19.(12分)已知函数![]() =
=![]()
(1)
求满足![]() =
=![]() 的所有
的所有![]() 值集合.
值集合.
(2)
若![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
20.(12分)一座大桥长1公里,车辆通过的最高限速为36公里/小时,为确保大桥安全,规定车辆通过大桥时相邻两车的最小车距![]() (米)与车速
(米)与车速![]() (米/秒)的立方成正比,当车速为10米/秒时,两车的最小车距为25米.现有某部队的一个车队,共25辆同一型号的大型汽车,车身长为a米,问:当首辆汽车进入桥头时,车队应以怎样的速度
(米/秒)的立方成正比,当车速为10米/秒时,两车的最小车距为25米.现有某部队的一个车队,共25辆同一型号的大型汽车,车身长为a米,问:当首辆汽车进入桥头时,车队应以怎样的速度![]() (米/秒)匀速前进,才能在最短时间内全部通过大桥?
(米/秒)匀速前进,才能在最短时间内全部通过大桥?
21.(12分) 已知两个函数![]() =
=![]() ,
,![]() ,其中k为实数.
,其中k为实数.
(1)
对任意的![]() ,都有
,都有![]()
![]() 成立,求k的取值范围;
成立,求k的取值范围;
(2)
对任意的![]() ,
,![]() 都有
都有![]() ,求k的取值范围.
,求k的取值范围.
22.(14分)已知连续函数![]() 是定义在R上的奇函数,
是定义在R上的奇函数, ![]() =2,
=2, ![]() 的导数
的导数![]() 在
在![]() 上恒大于0.
上恒大于0.
(1)
求当![]() 时,函数
时,函数![]() 的对应取值的集合;
的对应取值的集合;
(2)
解关于![]() 的不等式
的不等式![]()
![]() 且
且![]() ;
;
(3)
若![]()
![]() 对所有
对所有![]() 及
及![]() 均恒成立,求实数
均恒成立,求实数![]() 的取值范围.
的取值范围.