高三数学第一学期第二阶段测试

高三数学第一学期第二阶段测试

第Ⅰ卷（选择题）

一、　　　　　　 选择题：本大题共12小题，每小题5分，共60分；在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若函数（ D　 ）

　　　 A．0　　　　　　　　　　　　B．3　　　　　　　　　　　　C．-3　　　　　　　　　　　 D．3或-3

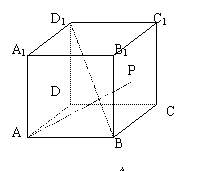2.如图：正方体中，点在侧面及其边界上运动，并且总保持，则动点的轨迹是 （B　　）

A．线段　B. 线段　

C. 中点与中点连成的线段　

 D. 中点与中点连成的线段

3．若四个正数a，b，c，d成等差数列，x是a和d的等差中项，y是b和c的等比中项，则x和y的大小关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　D  ）

　　　 A．x<y　　　　　　　　　　 B．x>y　　　　　　　　　　 C．x=y　　　　　　　　　　 D．x≥y

4、已知集合M={（x,y） y=}，N={（x,y） y=k（x+1）}当M∩N≠φ时k的取值范围是（　B　 ）

A、（∞， ] 　 B、[0，] 　　 C、[0，]　　　D、[0，]

5、ABCD-A₁B₁C₁D₁单位正方体，黑白两个蚂蚁从点A出发沿棱向前爬行，每走完一条棱称为“走完一段”。白蚂蚁爬地的路线是AA₁→A₁D₁→……，黑蚂蚁爬行的路线是AB→BB₁→……，它们都遵循如下规则：所爬行的第i+2与第i段所在直线必须是异面直线(其中i是自然数)。设白，黑蚂蚁都走完2003段后各停止在正方体的某个顶点处，这时黑，白两蚂蚁的距离是（ B　 ）

A、1　　　　  B、　　　　  C、　　　　　  D、0

6．若直线相切，则实数m的值等于　　　　　　 　　　　　　　（　 D ）

　　　 A．3或13　　　　　　　　B．3或-13　　　　　　　 C．-3或7　　　　　　　　D．-3或-13

9、已知函数，则的值是C

A、1　　　　　 B、2　　　　  C、3　　　　 D、4

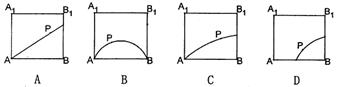
7、有一块“缺角矩形”木板ABCDE，其尺寸如图所示。欲用此木板锯成一块规则长方形木板，以下四种方案中哪种锯得的面积最大（　A　）

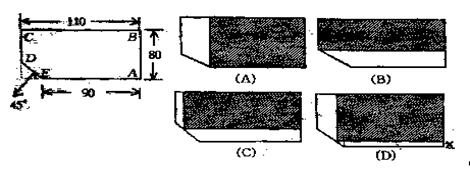8、数列满足并且。则数列的第100项为D

A、　　　 B、　　  C、　 　　 D、

10．定义在R上的偶函数，满足上是减函数，又α、β是锐角三角形的两个内角，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 C ）

A．　　　　　　　　　　　　 B．

C．　　　　　　　　　　　　D．

11．在正方体ABCD—A₁B₁C₁D₁的侧面AB₁内有一动点P到直线A₁B₁与直线BC的距离相等，则动点P所在曲线形状为 　　　　　　　　　　　　　　　　　　　 （　C  ）

12．某债券市场发行三种债券，A种面值为100元，一年到期本息和103元；B种面值为50元，半年到期本息和为51.4元；C种面值为100元，一年到期无利息，但买入价为97元，则这三种债券的收益率从小到大的排列为B　　　　　　　　　

　　　A．B，A，C　　　　　　　B．A，C，B　　　　　 C．A，B，C　　　　　　　D．C，A，B

第Ⅱ卷（非选择题共90分）

二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.

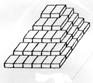
13,仓库有一种堆垛方式，如图（3）所示，最高一层2盒，第二层6

　　　 盒，第三层12盒，第四层20盒，……请你写在堆放层数n与盒

　　　 数的一个关系　　　　　　　　　　　 .

14,对于函数，给出下列四个命题：

　 ①存在； ②存在恒成立；

　 ③存在，使函数的图像关于y轴对称; ④函数的图象关于点对称；

　 其中正确命题的序号是　　　　　 

15.已知AB、CD是夹在两平行平面之间的两条线段，，AB=2,AB与平面成角，则线段CD的取值范围是________.

16．考察下列三个命题，是否需要在“　　　　”处添加一个条件，才能构成真命题（其中l，m为直线，α、β为平面）？如需要，请填这个条件，如不需要，请把“　　　　”划掉。

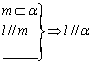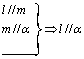　　① 　　 ② 　　③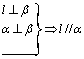

（注：此题最后得分是4分或0分）

三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.

17,知函数.

(1)化简的解析式； （2）若，求使为偶函数；

　 （3）在（2）成立的条件下，求满足=1 且 的ｘ集合．

18．（本小题满分12分）如图，在梯形ABCD中，AB∥CD，∠ADC=90°3AD=DC=3，AB=2，E是DC上一点，满足DE=1，连接AE，将△DAE沿AE折起到△D₁AE的位置，使得∠D₁AB=60°，设AC与BE的交点O.

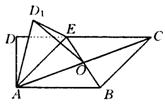
（Ⅰ）试用基向量

（Ⅱ）求异面直线OD₁与AE所成的角；

（Ⅲ）判断平面D₁AE与平面ABCE是否垂直？并说明理由.

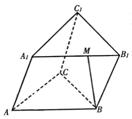
19,(满分12分）如图，三棱柱的底面是边长为2的等边三角形，

侧面ABB₁A₁是∠A₁AB=60°的菱形，且平面ABB₁A₁⊥ABC，

M是A₁B₁上的动点.

　 （1）当M为A₁B₁的中点时，求证：BM⊥AC；

　 （2）试求二面角A₁－BM－C的平面角最小时　　　

三棱锥M－A₁CB的体积.

20、乙两家电公司，2000年的市场占有率均为A，根据市场分析和预测，甲公司从2000年（第一年）起市场占有率与呈抛物线（如图一），乙公司自2000年起年的市场占有率都有所增加，规律如图二。

　　　　　　　　　　 　　　 图一　　　　　　　　　　　　　　　　　　　　　　　　　　　 图二　　　　　　　　　　

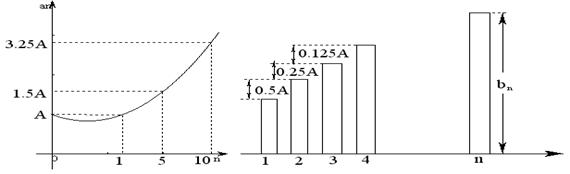
（1）　　根据两图信息，求出两公司第年市场占有率，的表达式。

（2）　　根据甲、乙两公司所在地的市场规律，如果某公司市场占有率不足另一公司市场占有率的20%，则该公司将被另一公司兼并，经计算2019年之前不会出现兼并局面，试问2019年是否会出现兼并局面，并说明理由。

21,函数f（x）在（－1，1）上有定义，且满足x、y∈（－1，1） 有

．

（1）证明：f（x）在（－1，1）上为奇函数；

（2）对数列求；

（3）求证

22. （本题满分14分）已知函数满足

,且使成立的实数是唯一的.

(1)　　  求函数的解析式、定义域、值域；

(2)　　  如果数列的前项和为，且，试求此数列的前3项，由此猜想数列的通项公式，并予以证明.