高三数学第一学期第二阶段测试答案
一.选择题: 学号_______ 姓名_______
1.D 2, A 3, D 4, B 5, B 6, D 7, C 8, A 9, D 10, C 11, C 12, B
二.填空题:13: ![]() _ ;
14:①③④ ; 15:_
_ ;
14:①③④ ; 15:_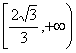 ;
;
16:_l![]() _a______
___l
_a______
___l![]() _a_____
__l
_a_____
__l![]() _a_______
_a_______
三.解答题:
17,知函数![]() .
.
(1)化简![]() 的解析式; (2)若
的解析式; (2)若![]() ,求
,求![]() 使
使![]() 为偶函数;
为偶函数;
(3)在(2)成立的条件下,求满足![]() =1 且
=1 且 ![]() 的x集合
的x集合
解:(1)由题得![]()
![]()
(2)当![]() 时,
时,![]() 为偶函数.
为偶函数.
(3)由![]() 得
得![]()
![]() 所求
所求![]() 的集合为
的集合为![]()
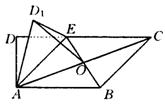
18.
|
(Ⅰ)试用基向量![]()
(Ⅱ)求异面直线OD1与AE所成的角;
(Ⅲ)判断平面D1AE与平面ABCE是否垂直?并说明理由.
解:(Ⅰ)根据已知,可得四边形ABCE为平行四边形.
所以,O为BE中点.
![]() (3分)
(3分)
(Ⅱ)![]()
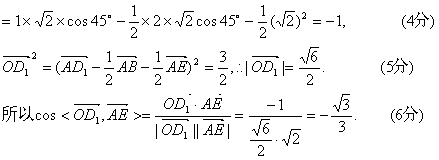
所以OD1与AE所成角为![]() (7分)
(7分)
(Ⅲ)设AE的中点为M,则![]()

|
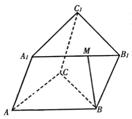
19,(满分12分)如图,三棱柱的底面是边长为2的等边三角形,
侧面ABB1A1是∠A1AB=60°的菱形,且平面ABB1A1⊥ABC,
M是A1B1上的动点.
(1)当M为A1B1的中点时,求证:BM⊥AC;
(2)试求二面角A1-BM-C的平面角最小时
三棱锥M-A1CB的体积.
解:(1)∵ABB1A1是菱形,∠A1AB=60°,且M为A1B1的中点,∴BM⊥A1B1,又A1B1∥AB,∴MB⊥AB.平面ABB1A1⊥平面ABC,∴MB⊥平面ABC.又AC![]() 平面ABC. ∴BM⊥AC ……4分 (2)作CN⊥AB于N,由于△ABC为正三角形,知N为AB为中点,又平面ABB1A1⊥平面ABC,∵CN⊥平面A1ABB1,作NE⊥MB于E点,连CE,由三垂线定理可知CE⊥BM,∴∠NEC为二面角A1—BM—C的平面角。…7分 由题意可知CN=
平面ABC. ∴BM⊥AC ……4分 (2)作CN⊥AB于N,由于△ABC为正三角形,知N为AB为中点,又平面ABB1A1⊥平面ABC,∵CN⊥平面A1ABB1,作NE⊥MB于E点,连CE,由三垂线定理可知CE⊥BM,∴∠NEC为二面角A1—BM—C的平面角。…7分 由题意可知CN=![]() ,在Rt△CNE中,
,在Rt△CNE中,![]() 要∠NEC最小,只要NE取最大值。又∵△A1B1B为正三角形,∴当M为A1B1中点时,MB⊥平面ABC,即E与B重合。此时NE取最大值且最大值为1,∴
要∠NEC最小,只要NE取最大值。又∵△A1B1B为正三角形,∴当M为A1B1中点时,MB⊥平面ABC,即E与B重合。此时NE取最大值且最大值为1,∴![]() ∴∠NEC的最小值为60° ……10分 此时
∴∠NEC的最小值为60° ……10分 此时![]() ……12分
……12分
.
20、乙两家电公司,2000年的市场占有率均为A,根据市场分析和预测,甲公司从2000年(第一年)起市场占有率![]() 与
与![]() 呈抛物线(如图一),乙公司自2000年起年的市场占有率
呈抛物线(如图一),乙公司自2000年起年的市场占有率![]() 都有所增加,规律如图二。
都有所增加,规律如图二。
图一 图二
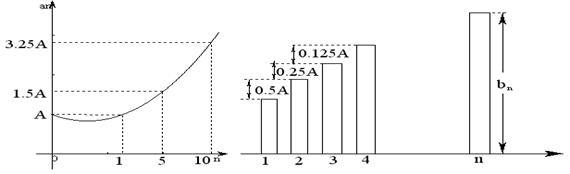

(1) 根据两图信息,求出两公司第![]() 年市场占有率
年市场占有率![]() ,
,![]() 的表达式。
的表达式。
(2) 根据甲、乙两公司所在地的市场规律,如果某公司市场占有率不足另一公司市场占有率的20%,则该公司将被另一公司兼并,经计算2019年之前不会出现兼并局面,试问2019年是否会出现兼并局面,并说明理由。
解:(1)由![]() (2分)
(2分)
设![]() 则
则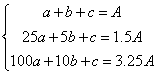 得:
得: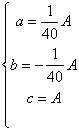
![]() (5分)
(5分)
由![]()
得 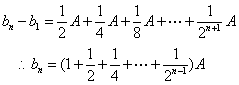
![]() (8分)
(8分)
(2)2019年,即经过20年时,
![]()
若出现兼并局面,则甲公司兼并乙公司。
此时![]()
∴到2019年,甲公司将兼并乙公司。 (14分)
21,函数f(x)在(-1,1)上有定义,![]() 且满足x、y∈(-1,1) 有
且满足x、y∈(-1,1) 有
![]() .
.
(1)证明:f(x)在(-1,1)上为奇函数;
(2)对数列![]() 求
求![]() ;
;
(3)求证![]()
讲解 (1)令![]() 则
则![]()
令![]() 则
则![]() 为奇函数.
为奇函数.
(2)![]() ,
, ![]()
![]() 是以-1为首项,2为公比的等比数列.
是以-1为首项,2为公比的等比数列.
![]()
(3)![]()
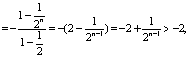
而 ![]()
![]()
本例将函数、方程、数列、不等式等代数知识集于一题,是考查分析问题和解决问题能力的范例. 在求解当中,化归出等比(等差)数列是数列问题常用的解题方法.
22. (本题满分14分)已知函数![]() 满足
满足![]()
![]() ,
,![]() 且使
且使![]() 成立的实数
成立的实数![]() 是唯一的.
是唯一的.
(1)
求函数![]() 的解析式、定义域、值域;
的解析式、定义域、值域;
(2)
如果数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,试求此数列的前3项,由此猜想数列的通项公式,并予以证明.
,试求此数列的前3项,由此猜想数列的通项公式,并予以证明.
解:![]()
![]()
有唯一解![]() 由
由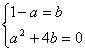 得
得![]()
![]() ,定义域为
,定义域为![]() , 值域为
, 值域为![]()
(2)![]()
![]()
![]()
![]() ,
, ![]()
相减得![]()
即:![]()
![]() .
.
猜想:![]() 用数学归类法证明之.
用数学归类法证明之.
(1)当n=1时,分式成立.
(2)假设n=k时公式成立,即:![]() ,
,
![]()
![]()
即n=k+1时分式也成立。 由(1)(2)知![]() 恒成立.
恒成立.