|
|
学科:数学 |
| 教学内容:高三数学第一学期期末综合检测 |
【同步达纲练习】
参考公式:
三角函数的和差化积公式
![]()
![]()
正棱台、圆台的侧面积公式 ![]()
其中c′、c分别表示上、下底面周长,l表示斜高或母线长
![]()
![]()
台体的体积公式:
![]()
其中S′、S分别表示上、下底面积,h表示高
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知(x,y)在映射f下的象是(x+y,x-y),则(1,2)的原象是
(A)![]() (B)
(B)![]()
(C)(2,1) (D)(2,-1)
(2)已知复数![]() ,则它的的共轭复数
,则它的的共轭复数![]() 的辐角主值是
的辐角主值是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(3)一个半径为5cm,圆心角为216°的扇形,卷成一个圆锥的侧面,则此圆锥的高是
(A)![]() (B)4cm
(B)4cm
(C)![]() (D)6cm
(D)6cm
(4)过点![]() 的直线l与直线x-y-1=0的交点在圆
的直线l与直线x-y-1=0的交点在圆![]() 上,则l的斜率为
上,则l的斜率为
(A)-2 (B)-2或0
(C)2 (D)2或0
(5)已知α、β、γ为三个不同的平面,a为一条直线,有下列四个命题:
①![]() ②
②![]()
③![]() ④
④![]()
其中正确的命题是
(A)①②④ (B)①④
(C)①③④ (D)②③
(6)双曲线![]() 的焦点到渐近线的距离是
的焦点到渐近线的距离是
(A)3 (B)4
(C)5 (D)6
(7)在数列![]() 中,
中,![]() ,则当前n项和取得最小值时的n的等于
,则当前n项和取得最小值时的n的等于
(A)3 (B)4
(C)3或4 (D)4或5
(8)若x、![]() ,3x+y=3,则
,3x+y=3,则![]() 的最大值是
的最大值是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(9)已知α、![]() ,
,![]() ,则
,则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(10)三年定期储蓄的年利率为2.7%(不计复利,即每年所得利息不计入本金),利息税为20%,某人三年后取款时得到税后利息2241元,则此人当时存入银行的金额在
(A)1至2万元之间 (B)2至3万元之间
(C)3至4万元之间 (D)4至5万元之间
(11)一个正方体的四个顶点都在一个半球的大圆面上,另四个顶点都在这个半球面上,若半球的体积为V,则正方体的体积为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(12)已知定义域为R的奇函数g(x),令f(x)=g(x)+k,其中k为常数,又f(-a)=m,则f(a)=
(A)2k-m (B)2k+m
(C)-2k+m (D)-2k-m
第Ⅱ卷(非选择题共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
(13)抛物线![]() 的准线方程是_________。
的准线方程是_________。
(14)从1,2,3,4,5中任取两个数,分别作为对数的底数和真数,则可以得到______个不同的对数值。
(15)把函数![]() 的图象沿x轴向左平移一个单位后,得到图象C,则C关于原点对称的图象的函数解析式为______.
的图象沿x轴向左平移一个单位后,得到图象C,则C关于原点对称的图象的函数解析式为______.
(16)长方体一个顶点上三条棱的长分别为a、b、c,(a、b、c两两不等),一条对角线为AB,长方体的表面上A、B两点间的最短路程为![]() ,则a、b、c的大小关系是________________。
,则a、b、c的大小关系是________________。
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤
(17)(本小题满分12分)
解关于x的不等式![]() (a>0,a≠1)
(a>0,a≠1)
(18)(本小题满分12分)
已知函数![]()
(Ⅰ)试判断函数f(x)在定义域上的单调性并用单调性定义证明;
(Ⅱ)若函数f(x)的反函数为![]() ,解方程:
,解方程:![]()
(19)(本小题满分12分)
已知:![]() ,cosαcosβ=cosα+cosβ,
,cosαcosβ=cosα+cosβ,
求:![]() 的值。
的值。
(20)(本小题满分12分)
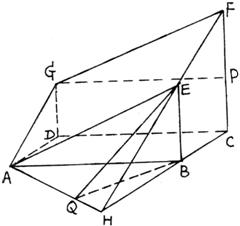
已知:如图所示的多面体是由底面为ABCD的长方体被截面AEFG所截而得的,其中AB=4,BC=1,BE=3,CF=4。
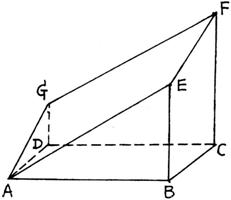
(Ⅰ)求异面直线EF与AD所成的角;
(Ⅱ)求截面AEFG与底面ABCD所成锐二面角的正切值;
(Ⅲ)求这个多面体的体积。
(21)(本小题满分12分)
已知等比数列的首项和公比皆为a,它的前n项和为![]()
(Ⅰ)求数列![]() 的前n项和
的前n项和![]() ;
;
(Ⅱ)求![]() 的值
的值
(22)(本小题满分14分)
斜率为![]() 的直线过椭圆
的直线过椭圆![]() (a>b>0)的右焦点F,与椭圆交于两点A、B,与y轴交于点C,且B为CF的中点,又A、B两点到右准线的距离之和为
(a>b>0)的右焦点F,与椭圆交于两点A、B,与y轴交于点C,且B为CF的中点,又A、B两点到右准线的距离之和为![]() ,求椭圆方程。
,求椭圆方程。

参考答案
【同步达纲练习】
一、(1)B(2)B(3)B(4)D(5)B(6)A(7)A(8)C(9)A(10)C(11)C(12)A
二、(13)![]() (14)13(15)
(14)13(15)![]() (16)a>b且a>c
(16)a>b且a>c
三、(17)解(一)令![]() ,则原不等式化为
,则原不等式化为
![]() …………………………………………………………2分
…………………………………………………………2分
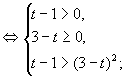 或
或![]() ……………………………………6分
……………………………………6分
![]() 或t>3
或t>3
![]() ……………………………………………………10分
……………………………………………………10分
即 ![]() ,
,
∴当0<a<1时,![]() ;当a>1时,
;当a>1时,![]() …………………………12分
…………………………12分
解(二)令![]() ,则
,则![]()
原不等式化为![]() ………………………………………………2分
………………………………………………2分
![]()
![]() 或t<-2(舍)………………………………6分
或t<-2(舍)………………………………6分
即![]()
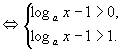
![]() …………………………………………10分
…………………………………………10分
∴当0<a<1时,![]() ;当a>1时,
;当a>1时,![]() …………………………12分
…………………………12分
(18)解:(Ⅰ)令![]() ,解得函数f(x)的定义域为-2<x<1……………………1分
,解得函数f(x)的定义域为-2<x<1……………………1分
令![]() ,则
,则
![]()
![]() …………………………3分
…………………………3分
![]() ,则
,则![]() ,
,![]() ,
,![]()
则![]() ,
,![]() 。
。
![]()
f(x)为定义域上的减函数………………………………8分
(Ⅱ)由![]() ,得
,得
![]() ………………………………10分
………………………………10分
即![]()
解得x=8
检验后,x=8为原方程的解…………………………12分
(19)解:由cosαcosβ=cosα+cosβ,得
![]() ……………………4分
……………………4分
![]() ………………8分
………………8分
令![]() ,又
,又![]() ,
,
则![]() ……………………………………10分
……………………………………10分
整理后,得![]()
解得 ![]() 或
或![]()
∴![]() …………………………………………12分
…………………………………………12分
(20)解:(Ⅰ)∵AEFG为截面,又平面ADG∥平面EBCF,
∴AG∥EF,∠GAD为所求。
可求得GD=4-3=1,
∴![]() ,
,
∠GAD=45°……………………4分
(Ⅱ)延长FE和CB,相交于H,连AH。作EQ⊥AH交AH于Q,连BQ。由三垂线定理,得BQ⊥AH。
则∠EQB为所求二面角的平面角………………6分
由EB:FC=HB:HC,得3:4=HB:(HB+1)
解得HB=3。
在Rt△ABH中,求得AH=5
由![]() ,可求得
,可求得![]() .
.
在Rt△EQB中,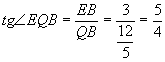 ………………………………9分
………………………………9分
(Ⅲ)再取一个与这个多面体一样的多面体,使截面对接,可组成一个长方体。
∴![]() ………………………………12分
………………………………12分
(21)解:(Ⅰ)由已知,a≠0.
当a=1时,![]() ,
,
![]() …………………………2分
…………………………2分
当a≠1时,![]()
![]()
![]()
![]()
![]() ……………………………………………………6分
……………………………………………………6分
(Ⅱ)当a=1时,![]()
![]()
∴![]() …………………………………………9分
…………………………………………9分
当a≠1时,![]()
无论a<1还是a>1,当![]() 时,都有
时,都有
![]()
∴![]() …………………………………………………………12分
…………………………………………………………12分
(22)解:设椭圆右焦点为(c,0),则直线方程为![]()
令x =0,求得点C的坐标为![]()
由中点坐标公式求得B点坐标为![]() ………………………………2分
………………………………2分
由点B在椭圆上,得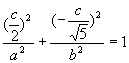 。
。
把![]() 代入,解得
代入,解得![]() ……………………………5分
……………………………5分
又设![]()
解方程组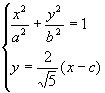
代入消去y并整理,得
![]()
∴![]()
将![]() 代入并整理,得
代入并整理,得![]() ………………………………8分
………………………………8分
由已知,![]()
![]() ………………………………10分
………………………………10分
由![]() 及
及![]() 得c=2b.
得c=2b.
代入上式,得![]()
解得 b=1, ∴![]()
则![]() 为所求…………………………………………14分
为所求…………………………………………14分
