高三数学模拟试题5

高三数学模拟试题5

一、选择题：(本题共12小题，每小题5分，共60分)在每个小题给出的四个选项中，只有一个是正确的。

1、已知曲线C：tx²+(1－t)y²=1表示双曲线，则实数t的取值范围为(　　 )

(A)0＜t＜1　　　　　　　　　 (B) t＜0或t＞1　　　　　　(C)t＜1且t≠0　　　　　　 (D)t＞1

2、已知a、b为实数且a＞b，则下列不等式一定成立的是(　　 )

(A)a²＞b²　　　　　　　　　　 (B)＜1　　　　　　　　　　　　　　(C)lg(a－b)＞0　　　　　　 (D)

3、下列函数中最小正周期为的函数是(　　 )

(A) y=sin4x　　　　　　　　　 (B) y= tan(2x－1)　 　　 (C) y=cosx+2　　　　　　　 (D) y=－sinx

4、已知向量=(1－,1)与向量=(2,)互相垂直，则实数的值为(　　)

(A)　　　　　　　　　　　　　 (B)1 　　　 　　　 　　　　　　　(C)2 　　　　　　　　　　 　　　 (D)－1或2

5、已知函数f(x)(x∈R)存在反函数，且函数f(x)的图象经过点(0,－1)，那么函数f (x+3)的反函数必经过点(　　 )

(A) (－4,0)　　　　　　　　　 (B) (－1,－3)　　　　　　　　(C) (－3,－1)　　　　　　　 (D) (－1, 3)

6、设O为坐标原点，抛物线y²=2x与过焦点的直线交于A、B两点，则=(　　 )

(A)　　　　　　　　　　　　　 (B)－　　　　　　　　　　　 (C)3　　　　　　　　　　　　　　 (D)－3

7、设x、y∈R，则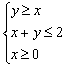所围成的图形的面积为(　　 )

(A)4　　　　　　　　　　　　　　 (B)3　　　　　　　　　　　　　　 (C)2　　　　　　　　　　　　　　 (D)1

8、已知在直角三角形ABC中，∠C=90°，sinA、sinB为方程4x²+4mx+1=0的两根，则实数m的值为(　　 )

(A)－　　　　　　　　　　　 (B)－2　　　　　　　　　　　　 (C)±2　　　　　　　　　　　　　 (D)

9、若关于x的不等式x－1＜ax的解集中恰有两个整数，则实数a的取值范围为(　　 )

(A)()　　　　　　　　　　(B)　　　　　　　　　　(C)　　　　　　　　　　(D)

10、一直线型公路沿途设有21个商业网点，从左到右分别称为1、2、…、21号网点，且相邻的每两个网点之间的距离相等，现准备从21个网点中选择一个设立批发中心，为使各网点到该中心的往返路程的所有总和最小，则批发中心应设立在从左到右的(　　 )号网点

(A)1或21　　　　　　　　　　(B)10或11　　　　　　　　　 (C)11　　　　　　　　　　　　　 (D)任意

11、如果圆x²+y²=2k²至少覆盖函数f(x)=3sin的一个最大值点和一个最小值点，则实数k的取值范围为(　　 )

(A)k≤3 且k≠0　　　　　(B)k≥3　　　　　　　　　　　(C)k≥　　　　　　　　　(D)k≤且k≠0

12、设直线nx+(n+1)y=(n∈N )与两坐标轴所围成的图形的面积为S_n(n=1,2,…,2004)，则S₁+S₂+…+S₂₀₀₄的值为(　　 )

(A)　　　　　　　　　　 (B)　　　　　　　　　　　　　　(C)　　　　　　　　　　　　　　(D)1

二、填空题：本题共有4小题，每题4分，共16分，请将答案填在答卷对应横线上。

　　13、已知=arc cos()，则tan()的值为__________．

　　　 14、已知等差数列{a_n}中a₁=1，a₆+a₁₀=18－a₈，则a₅₀ =__________．

　　　 15、焦点在x轴上的椭圆有一内接等腰直角三角形ABC，椭圆的两焦点在⊿ABC的两腰上，且直角顶点A(0,2)为椭圆短轴的一个端点，则⊿ABC的面积为____________．

　　　 16、定义在R上的函数y=f(x)具有下述性质：

　　　 ①对任何x∈R，都有f(x³)=f ³(x)；②对任何实数x₁、x₂，如x₁≠x₂，都有f(x₁)≠f(x₂)．

则f(－1)+f(0)+f(1)=__________．

三、解答题：本题共有6个小题，共74分，要求写出具体推理过程与演算步骤。

17、(本小题满分12分)

已知数列{a_n}满足a_n+1²=a_na_n+2(n∈N ^*)，a₃=27,a₆=1．

(1)求数列{a_n}的通项公式；

(2)令b_n=log₃ a_n，求数列{b_n}的前n项和S_n．

18、(本小题满分12分)

已知f(x)=log(sinxcosx－cos²x+)．

(1)试确定f(x)的定义域与值域；

(2)求f(x)的单调递增区间．

19、(本小题满分12分)

已知有两个函数f(x)=, g(x)=2x．

(1)求函数h(x)=f(x)·g(x)的最大值，并求对应的x的值；

(2)解关于x的不等式f(x)≥g(x)．

20、(本小题满分12分)

某库区有座水库，其设计的最大库存容量是26.2万方，此库区的森林覆盖率为60%，除林地外其余的为裸露地，如有降雨，则林地和裸露地分别有10%和85%的雨水变成地表水流入水库，经预测有连续降雨，且单位面积降雨量相同，库区在开始降雨的x天内降雨的总水量为y(万方)与天数x之间的函数关系式为y=(x∈N ^*，x＜30)．经测得在开始降雨的6天内库区的降雨的总水量为6万方．水库原有水量20万方，在降雨的第二天就开始泄洪，每天泄洪量为0.2万方．

(1)求p的值；

(2)连续降雨多少天后，该水库会发生险情(水库里的水量超过设计的最大库容量就有危险)．

21、(本小题满分12分)

已知有一离心率为，中心在原点、焦点在x轴上的圆锥曲线C，它的一个焦点到相应准线的距离为；已知有一定点A(0,－1)，另有一条在y轴上的截距为m的直线l与曲线交于相异两点M、N．

(1)求曲线C的方程；

(2)如AM=AN，求实数m的取值范围．

22、(本小题满分14分，文科做1、2小题，理科做1、2、3小题)

已知f(x)=(a＞0,a≠1)．

(1)求f ^－1(x)；

(2)求证：y=f(x)的图象关于点P()对称；

(3)设a_n=，b_n=，是否存在实数a，对n∈N ^*都有a_n+1＞b_n恒成立，若存在，求出a的范围，若不存在，请说明理由.

一、BDCCB、BDABC、BB　　　　　　　　　 二、13、7；14、36；15、；16、 0 ．

三、17、(1){a_n}为等比数列，公比q=，a₁=3⁵，a_n=3^6－n；(2)b_n=6－n，{b_n}为等差数列，则S_n=．

18、f(x)=1+=+

(1)令＞0，得x∈() (k∈Z)

由∈(0,1]，∴∈[0,+∞)，∴f(x)∈[,+∞)．

(2)令 (k∈Z)．

19、(1)h(x)的定义域为[－2,2],当x∈[－2,0]时,h(x)≤0;当x∈(0,2]时,h(x)=2x≤2≤,当且仅当x=时取得;(2) f(x)≥g(x),即≥2x，∴当x∈[－2,0]时,显然成立;当x∈(0,2]时,平方,解得x∈(0,],综合有,x∈[－2,]．

20、(1)p=30；(2)设在开始降雨的x天内不会发生险情，则有y(60%·10%+40%·85%)+20－0.2(x－1)≤26.2

有0.4y－0.2x≤30,即2≤x+30,∵x≥1,∴1≤x≤10,故连续降雨10天后该水库会发生险情。

21、(1)+y²=1;(2)显然l的斜率存在，设l:y=kx+m,代入椭圆方程，有(3k²+1)x²+6kmx+3m²－3=0，解得线段MN的中点的坐标为P(,)，由题，AP⊥MN则有3k²=2m－1……①，且由于⊿＞0，解得3k²－m²+1＞0……②将①代入②式，解得m∈(0,2)．

22、(1)f ^－1(x)=(0＜x＜1);(2)欲证明结论，即证明f(x)关于点P()的对称曲线即为f(x)，设f(x)关于点P的对称曲线上一点(x,y)，则(1－x,1－y)在f(x)上，有1－y=,得y=,知结论成立．

(3)a_n=a ^-n, b_n==1+,对n∈N ^*都有a_n+1＞b_n恒成立，即a ^-n＞恒成立，

①a＞1时，有－n＞恒成立，a＞,∵0＜≤1, ∈(0, ],

∴a＞,综合条件有a＞；②0＜a＜1时，有－n＜恒成立，a＜，得a≤0, 综合条件0＜a＜1,无解．综合①②，存在这样的实数a ,当a＞时，对n∈N ^*都有a_n+1＞b_n恒成立．