高三数学模拟题(文科1)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1).设P={3,4,5},Q={4,5,6,7},定义P※Q=![]() ,则P※Q中元素的个数为 ( )
,则P※Q中元素的个数为 ( )
(A).3 (B).4 (C).7 (D).12
(2).已知向量![]() 的值是( )
的值是( )
(A).![]() (B).
(B).![]() (C).
(C).![]() (D).1
(D).1
(3).已知函数![]() 的图象与其反函数的图象有交点,且交点的横坐标为
的图象与其反函数的图象有交点,且交点的横坐标为![]() ,
,
则有 ( )
(A).![]() (B).
(B).![]()
(C).![]() (D).
(D).![]()
(4).设F1,F2是双曲线![]() 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且![]() ,
,
则![]() 的值等于 ( )
的值等于 ( )
(A).2 (B).![]() (C).4 (D).8
(C).4 (D).8
(5).下列四个函数中,在区间(0,1)上为增函数的是 ( )
(A).![]() (B).
(B).![]() (C).
(C).![]() (D).
(D).![]()
(6).若0为平行四边形ABCD的中心,![]() 等于( )
等于( )
(A).![]() (B).
(B).![]() (C).
(C).![]() (D).
(D).![]()
(7).在等比数列![]() ( )
( )
(A).![]() (B).
(B).![]() (C).
(C).![]() (D).
(D).![]()
(8).已知集合![]() 则M中只含二个元素的子集的
则M中只含二个元素的子集的
个数为( )
(A).3 (B).15 (C).21 (D).42
(9).设函数f (x)的定义域为D,如果对于任意的![]() ,使
,使
![]() 成立,则称函数f (x)在D上均值为C,给出下列四个函数①
成立,则称函数f (x)在D上均值为C,给出下列四个函数①![]() ②
②![]() ③
③![]() ④
④![]()
则满足在其定义域上均值为2的所有函数是 ( )
(A).①② (B).③④ (C).②④ (D).①③
(10).设偶函数![]() 的大小关系是 ( )
的大小关系是 ( )
(A).![]() (B).
(B).![]()
(C).![]() (D).不能确定
(D).不能确定
(11).已知![]() 则不等式
则不等式![]() (
(
(A)![]() (B)
(B)![]() (C)
(C)![]() (D).
(D).![]()
![]()
![]()
(12).若一个圆的圆心在抛物线![]() 的焦点处,且此圆与直线
的焦点处,且此圆与直线![]() 相切,则这个圆的方程是 ( )
相切,则这个圆的方程是 ( )
(A).![]() (B).
(B).![]()
(C).![]() (D).
(D).![]()
二、填空题(本题共4小题,每小题4分,共16分)
(13). y=sinx在0≤x≤2π与x轴所围成图形的面积S=
(14).已知椭圆![]() 与双曲线
与双曲线![]() 有相同焦点,则实数t=
有相同焦点,则实数t=
(15).给出以下命题①存在实数x使sinx+cosx=![]() ;②若α、β是第一象限角,且α>β,则cosα<cosβ;③函数y=sin(
;②若α、β是第一象限角,且α>β,则cosα<cosβ;③函数y=sin(![]() )是偶函数;④若cosαcosβ=1,则sin(α+β)=0;⑤将y=sin2x图象向左平移
)是偶函数;④若cosαcosβ=1,则sin(α+β)=0;⑤将y=sin2x图象向左平移![]() 个单位得到的是函数y=sin(
个单位得到的是函数y=sin(![]() )的图象,其中正确命题的序号是
)的图象,其中正确命题的序号是
(16).已知奇函数满足f(x+1)=-f(x),当x∈(0,1)时,f(x)=2x,
则x∈(-3,-2)时f(x)=
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
三、解答题:本大题共5小题;共54分. 解答应写出文字说明、证明过程或演算步骤.
(17)(10分)已知![]()
(18).(12分)设![]()
(19).(12分)已知函数![]()
(1)当a=-1时,求函数f (x)的最大值和最小值.
(2)求实数a的取值范围,使![]() 上是单调函数.
上是单调函数.
(20).(12分)设![]() 、
、![]() 是两个不共线的非零向量(t∈R)
是两个不共线的非零向量(t∈R)
①若![]() 与
与![]() 起点相同,t为何值时,
起点相同,t为何值时,![]() ,t
,t![]() ,
,![]() (
(![]() +
+![]() )三向量的终点在一直线上?
)三向量的终点在一直线上?
②若![]() =
=![]() 且
且![]() 与
与![]() 夹角为60°,那末t为何值时
夹角为60°,那末t为何值时![]() -t
-t![]() 的值最小?
的值最小?
(21).(12分)王先生因病到医院求医,医生给开了处方药(片剂),要求每天早晚各服一片,已知该药片每片220毫克,他的肾脏每12小时从体内排出这种药的60%,并且如果这种药在他体内的残留量超过386毫克,就将产生副作用,请问:
(I)王先生第一天上午8时第一次服药,则第二天早晨8时服完药时,药在他体内的残留量是多少?
(II)如果王先生坚持长期服用此药,会不会产生副作用,为什么?
(22).已知二次函数![]()
x1、x2.
(1)如果![]()
(2)若![]() (14分)
(14分)
高三数学模拟题答案(文科1)
一、选择题:
(1)D (2) D (3) B(4)A(5)B(6) B(7)C(8)C(9)B(10)C(11)C (12)A.
二、填空题:
(13). 4 (14).1 (15).③④ (16).2-x-2
二、解答题:
(17).解:![]()
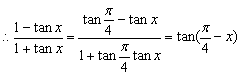
![]()
![]()
(18).解:(1)当![]() .
.
故不等式可化简为![]()
又![]() 故此时不等式的解为:
故此时不等式的解为:![]()
(2)当a>1时,即![]() 时,
时,
不等式可变为![]() 两边平方解得:
两边平方解得:![]()
故此时不等式的解为:![]()
综上(1)(2),原不等式解集为:![]()
(19).解:(1)1,37 (2)![]()
(20).①设![]() -t
-t![]() =m[
=m[![]() -
-![]() (
(![]() +
+![]() )](m∈R) 化简得
)](m∈R) 化简得![]()
![]() =
=![]()
![]()
∵![]() 与
与![]() 不共线 ∴
不共线 ∴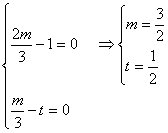
∴t=![]() 时,
时,![]() 、t
、t![]() 、
、![]() (
(![]() +
+![]() )终点在一直线上
)终点在一直线上
②![]() -t
-t![]() 2=(
2=(![]() -t
-t![]() )2=
)2=![]() 2+t2
2+t2![]() -2t,
-2t,
![]()
![]() cos 60°=(1+t2-t)
cos 60°=(1+t2-t)![]() 2, ∴t=
2, ∴t=![]() 时,
时,![]() -t
-t![]() 有最小值
有最小值![]()
(21).解:(I)设第n次服药后,药在他体内的残留量为![]() 毫克,依题意,
毫克,依题意,
![]()
![]() (毫克),
(毫克),
第二天早晨是他第三次服药,故服药后药在体内的残留量为343.2(毫克)
(II)依题意,![]()
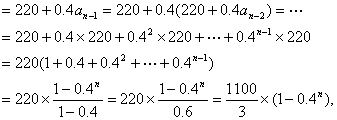
若长期服药,药在体内的残留量为![]()
∴不会产生副作用
(22).
