高三第一章概率与统计单元测试题(理)
一、 选择题 (每小题5分,共12小题,每小题有且只有一个正确的答案)
1. 下列随机变量中,不是离散随机变量的是 ( )
A. 从10只编号的球 ( 0号到9号) 中任取一只,被取出的球的号码
B. 抛掷两个骰子,所得的最大点数
C. [0 , 10]区间内任一实数与它四舍五入取整后的整数的差值
D. 一电信局在未来某日内接到的 电话呼叫次数
2. 某批量较大的产品的次品率为10%,从中任意连续取出4件,则其中恰好含有3件次品的概率是
A. 0.0001 B. 0.0036 C. 0.0486 D. 0.2916 ( )
3. 已知随机变量的分布列为
|
| －1 | 0 | 1 |
| P | 0.5 | 0.3 | 0.2 |
则最可能出现的值是
( )
A. 0.5 B. －1 C. 0 D. 1
4. 有N件产品,其中有M件次品,从中不放回地抽n 件产品,抽到的次品数的数学期望值是
A.
n
B. 
C. 
D. 
( )
5. 设是随机变量,且
,则
等于
( )
A. 0.4 B. 4 C. 40 D. 400
6. 已知随机变量服从二项分布
,则P(=2) =
( )
A. 
B. 
C. 
D. 
7. 在某餐厅内抽取100人,其中有30人在15岁以下,35人在16至25岁,25人在26至45岁,10人在46岁以上,则数 0.35 是16到25岁人员占总体分布的 ( )
A. 概率 B. 频率 C. 累计频率 D. 频数
8. 设有一个直线回归方程为
,则变量x 增加一个单位时
( )
A. y 平均增加 1.5 个单位 B. y 平均增加 2 个单位
C. y 平均减少 1.5 个单位 D. y 平均减少 2 个单位
9. 某服务部门有n 个服务对象,每个服务对象是否需要服务是独立的,若每个服务对象一天中需要服务的可能性是 p , 则该部门一天中平均需要服务的对象个数是 ( )
A . n p (1－p) B. n p C. n D. p (1－p)
10. 设有n 个样本
,其标准差是
,另有n个样本
,且
( k = 1, 2, … , n ),其标准差为
,则下列关系正确的是
( )
A. 
.B. 
C. 
D. 
11. 已知随机变量的概率密度函数为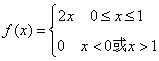
,则
A. 
B. 
C. 
D. ( )
12. 某单位有老年人28 人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36样本,适合的抽取样本的方法是 ( )
A. 简单的随机抽样 B. 系统抽样
C. 先从老年中排除一人,再用分层抽样 D.分层抽样
二、填空题 ( 每小题4分,共4个小题,16分)
13. 一个容量为20的样本数据,分组后,组距与频数如下: 
,2; 
, 3 ; 
, 4 ; 
, 5 ; 
, 4 ; 
, 2 .则样本在区间 
上的频率为_______________________
14. 一射手对靶射击,直到第一次中靶为止.他每次射击中靶的概率是 0.9 ,他有3颗弹子,射击结束后尚余子弹数目的数学期望
=______________________
15. 有一个简单的随机样本: 10, 12, 9, 14, 13
则样本平均数
=__________ ,样本方差
=___________
16. 设随机变量
,则可知 
_________________
三、解答题( 共6 小题,总分74分,要求写出必要的解题过程 )
17. (本题满分12分)
假定每人生日在各个月份的机会都是相等的,
求: (1) 某班的60个人中生日在一月份的平均人数;
(2) 该班的60个人中有2人生日在第一季度的概率(只列出式子即可)
18. (本题满分12分)
已知随机变量的分布列为
|
| １ | ２ | ３ |
| P |
|
|
|
且已知 
, 求: (1) 
,
,
(2) 
, 
19. (本题满分12分)
甲、乙两名射手在一次射击中的得分是两个随机变量,分别记为和
,它们的分布列分别为
|
| ０ | １ | ２ |
| P | ０.1 | a | 0.4 |
|
| 0 | 1 | 2 |
| P | 0.2 | 0.2 | b |
(1) 求a , b 的值
(2) 计算和的期望与方差,并以此分析甲、乙两射手的技术情况.
20. (本题满分12分)
若随机事件Ａ在一次试验中发生的概率为Ｐ ( ０<Ｐ<１ ),用随机变量表示Ａ在一次试验中发生的次数. (1) 求方差
的最大值;
(2) 求
的最大值.
21. (本题满分12分)
已知测量误差
(单位:㎝ ),
.
(１) 求一次测量中误差的绝对值不超过8 ㎝ 的概率;
(２) 必须进行多少次测量才能使至少有一次测量的误差的绝对值不超过8 ㎝ 的概率大于 0.9 ?
22. (本题满分14分)
从一批有5个合格品与3个次品的产品中,一件一件地抽取产品,设各个产品被抽到的可能性相同.记为直到取出的是合格品为止时所需抽取的次数,分别在下列三种情形下求出:
(1) 每次抽取的产品都不放回到这批产品中的的分布列和所需平均抽取的次数;
(2) 每次抽取的产品都立即放回到这批产品中,然后再抽取一件产品的的分布列;
(3) 每次抽取一件产品后,总将一件合格品放入这批产品中的的分布列.
参考答案:
一、选择题
Ｃ Ｂ Ｂ Ｃ Ａ ,Ｄ Ｂ Ｃ Ｂ Ｂ ,Ｄ Ｃ
二、填空题
13.
0.7
14. 1.89 15. 11.6 , 3.44 16. 
三、解答题
17. (1) 5 (2) 
18. (1) 0.25 , 0.5 , 0.25 (2) 0.25 , 0
19. (1) a = 0.5 b = 0.6 (2) =1.3 =0.41 
= 1.4 
= 0.64
两者比较略去.
20. (1) p = 
时, 的最大值为 (２)
时,最大值为
21. (1) 0.567 (2) 至少 3 次 .
22. (1)
|
| 1 | 2 | 3 | 4 |
| P |
|
|
|
|
= 1.5
(2)
(3) 略