高三模拟测试数学试题

高三模拟测试数学试题

本试卷分第I卷和第II卷两部分，满分150分，考试时间120分钟。

第I卷（选择题 共60分）

一、选择题（本大题12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1．已知集合则　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　B．

　　　 C．A=B　　　　　　　　　　　　　　　　　　　　　　　　　 D．

2．函数的图象　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．关于直线y=0对称　　　　　　　　　　　　　　　B．关于直线x=0对称

　　　 C．关于直线y=1对称　　　　　　　　　　　　　　　D．关于直线x=1对称

3．△ABC中，若2cosASinB=SinC，则△ABC的形状一定是　　　　　　　　　　　　　　　　　　（　　）

　　　 A．等腰直角三角形　　　　　　　　　　　　　　　　 B．直角三角形

　　　 C．等腰三角形　　　　　　　　　　　　　　　　　　　　D．等边三角形

4．下面的四个命题　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 ①　　　　　　　　　　　　　　　　　　 ②

　　　 ③若　　　　　　　　 ④若

　　　 其中真命题是

　　　 A．①②　　　　　　　　　 B．③④　　　　　　　　　 C．①③　　　　　　　　　 D．②④

5．点M（x_0，y₀）是圆x²+y²=a²(a>0)内异于圆心的点，则直线x₀x+y₀y=a²与该圆的位置关系是　　　　　　　　　　　　　（　　）

　　　 A．相切　　　　　　　　　 B．相交　　　　　　　　　 C．相离　　　　　　　　　 D．相切或相交

6．（理）设复数2+3i的幅角主值为θ，则6－4i的幅角主值为　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　B．　　　　　　　　C．　　　　　　　D．－θ

6．（文）抛物线y²=p（x+1）的准线方程为x=－3，该抛物线的焦点坐标是　　　　　　 （　　）

　　　 A．（1，0）　　　　　　　B．（2，0）　　　　　　　C．（－1，0）　　　　　D．（－2，0）

7．S_n表示等差数列{a_n}的前n项和，若则等于　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　 C．　　　　　　　　　　　D．

8．把直线x+y－1=0沿y轴正方向平移1个单位再关于原点对称后，所得直线的方程是（　　）

　　　 A．­x+y+2=0　　　　　　 B．­x－y－2=0　　　　　C．­x+y－2=0　　　　　 D．­x－y+2=0

9．一个正方体内接于一个球，过球心作一截面，则截面的图形不可能是　　　　　　　　（　　）

　　　　　　　　　　　　 A．　　　　　　 B．　　　　　　　 C．　　　　　　 D．

10．若函数y=f(x)的图象和的图象关于直线对称，则f（x）的表达式为　　　　　　　　　　　　 （　　）

　　　 A．　　B．　　　 C．　　　 D．

11．从如图放置的球体容器顶部的一个孔向球内以相

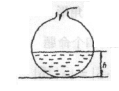
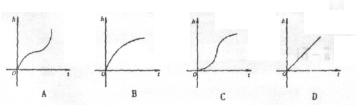
同的速度注水，容器中水面的高度h与注水时间t

　　之间的关系用图象表示应为

12．如果一个三位正整数a₁a₂a₃满足a­₁<a₂且a₃<a₂,则称这样的三位数为凸数（如120、363、374等），那么所有凸数的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．240　　　　　　　　　　 B．285　　　　　　　　　　 C．729　　　　　　　　　　 D．920

第II卷（非选择题 共90分）

二、填空题（本大题共4个小题，每小题4分，共16分，请把答案直接写在横线上）

13．若a>b>0，且则m的取值范围是　　　　　　　 .

14．若展开式中含有常数项，则n的最小值是　　　　  .

15．球面上有四点P、A、B、C，如果PA、PB、PC两两垂直且PA=PB=PC=a，那么球的表

面积是　　　　　　

16．已知F为抛物线y²=2ax的焦点，P为此抛物线上任一点，O为坐标原点，以下四个命题：

　　　 ①△FOP为等边三角形　　　　　　　　　　　　　　②△FOP为等腰直角三角形

　　　 ③△FOP为直角三角形　　　　　　　　　　　　　　④△FOP为等腰三角形

　　　 其中一定不正确的命题的序号是　　　　  .

三、解答题（本大题6个小题，共74分，解答应写出必要的文字说明、证明过程及演算步骤）

17．（本小题满分12分）

甲、乙、丙三人独立参加入学考试合格的概率分别为

　 求：（1）三人中恰有两人合格的概率;

　　　（2）（理科做）合格人数ξ的数学期望.

（文科做）三人中至少有一人合格的概率.

 

18．（本小题满分12分）

　 设

　 解不等式.

19．（本小题满分12分）

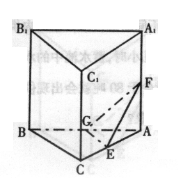
　　如图在直三棱柱ABC—A₁B₁C₁中，AC=BC=AA₁=2，∠ACB=90°，E、F、G分别为AC

AA₁，AB的中点.

①求证：B₁C₁//平面EFG;

②（理科做）求FG与AC₁所成的角;

③（文理科都做）求三棱锥B₁——EFG的体积.

20．（本小题满分12分）

　　某自来水厂的蓄水池中存有400吨水，水厂每小时可向蓄水池中注入60吨水，同时蓄

水池又向居民小区不间断地供水，t小时内供水总量为120吨（0≤t≤24）

　　（1）从供水开始到第几小时，蓄水池中的水量最少？最少水量有多少吨？

（2）若蓄水池中水量少于80吨就会出现供水紧张现象.试问：在一天的24小时内，有

几个小时会出现供水紧张现象？

21．（本小题满分12分）

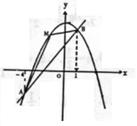
 设抛物线y=4－x²与直线y=3x的交点为A、B，点M在抛物线的AB弧上运动，设

S_△MBA达到最大值时，点M的坐标为（p，h）.

（1）求过点（p，h）的切线方程;

（2）（理科做）证明：直线AB与抛物线y=4－x²所围成的图形面积被x=p平分.

　　　　（文科做）证明：若与直线AB平行的直线截抛物线y=4－x²的弦为CD，则CD被直线x=p平分.

 22．（本小题满分14分）

　　 已知等比数列{a_n}中，

　　（1）求数列{a_n}的通项公式;

（2）求;

（3）设S_n是等比数列{a_n}的前n项的和，是否存在这样的自然数n，使成立，若存在，求出n的值；若不存在，请说明理由.

高三年级模拟测试

数学试题参考答案及评分标准

一、  选择题

1.D　2.D　3.C  4.B　5.C　6.A  7.B　8.A　9.D  10.B　11.A　12.A

二、填空题

13.－b<m<0　　14.5　 15.3πa²　　16.①②

三、解答题

17.（文）（1）用A、B、C分别表示甲、乙、丙入学考试合格，由题意知，事件A、B、C相互独立，三个中恰有两人合格包括三种情况：、、，这三者间彼此互斥，故

……（12分）

……（6分）

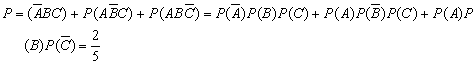
（2）

（理）（1）参考文科

　　 （2）考试合格人数的分布列为

ξ	0	1	2	3
P

	……（10分）

……（12分）

　　　　　  

18.解：

 （1）当0<a<1即－1<x<0时　x+2>0　 x－4<0　……3分

　 故不等式可化简为x+2<4－x解得x<1 ……4分 又－1<x<0　故此时不等式解为：－1<x<0　……6分

 （2）当a>1时，即x<－1或x>0 则当x≠－2且x≠4时……8分　不等式可变为x+2>x－4 两边平方解得：x>1　……10分 故此时不等式解为x>1且x≠4时…11分

　综上（1）（2）原不等式解集为：（－1，0）∪（1，4）∪（4，+∞）……（12分）

19. ①证明：∵E、G分别为AC、AB中点 ∴EG//BC//B₁C₁　即B₁C₁//EG　……（2分）

而B₁C₁平面EFG　EG平面EFG　∴B₁C₁//平面EFG……（4分）

②BC⊥平面AA₁C₁C　A₁B在平面AA₁C₁C的射影为A₁C……（6分）

即FG与AC₁所成的角为90^。……（7分）

③连AC₁交EF于H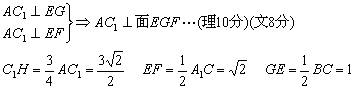　

……（12分）

20.解：设t小时后蓄水池中的量为y吨，则……（2分）

　 令 当x=6 即t=6时，y_min=40

故从供水开始到第6小时的时候，蓄水池中水量最少，只有40吨……（6分）

（2）由400+10x²－120x<80即 …（10分） 在一天的24小时内，有8个小时供水紧张……（12分）

21.解（1）由 解得 x=－4　x=1……2分

　　AB长度确定，要使S_△MAB最大，只需M到直线AB的距离最大，则M（x，y）到直线AB的距离

　　当时，d达到最大……（4分）即p=

 故过点M

的切线方程为：即12x－4y+25=0…（6分）

（2　　　　 文科）证明 设与AB平行的直线截抛物线的弦CD所在直线

的方程为：y=3x+b 由…（文8分）

　  则CD中点的横坐标为 即CD被直线平分…（文12分）

（2　理科）证明：直线AB与抛物线所围成的图形的面积为：

 …（理10分）而

 可见，直线AB与抛物线所围成的图形的面积被平分……（理12分）

22.（1）由题设

　解得……（4分）

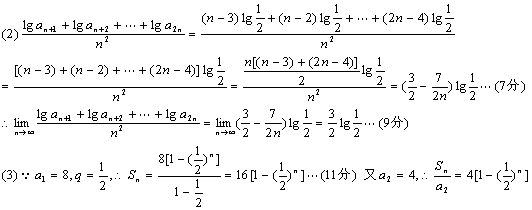
假设存在自然数n，使成立 则

 故存在自然数n，使成立，此时n=4（14分）